
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 26 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
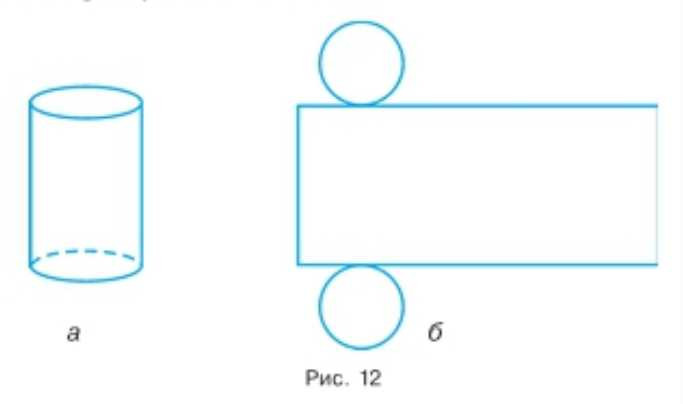
На рисунке 12, а изображён цилиндр. Сверху и снизу цилиндр ограничен кругами, которые называются основаниями цилиндра. Развёртка боковой поверхности цилиндра — прямоугольник. На рисунке 12, б изображена развёртка поверхности цилиндра. Попробуйте вычислить площадь поверхности цилиндра, если его высота 5 см, а радиус оснований 2 см.
Так как высота цилиндра равна ширине прямоугольника, длина прямоугольника равна длине окружности основания цилиндра:
\(2 \pi r = 2 \cdot 3,14 \cdot 2 = 12,56 \, (\text{см})\).
Площадь боковой поверхности:
\(5 \cdot 12,56 = 62,8 \, (\text{см}^2)\).
Площадь двух оснований (площадь круга):
\(S = 2 \pi r^2 = 2 \cdot 3,14 \cdot 2^2 = 25,12 \, (\text{см}^2)\).
Площадь поверхности цилиндра:
\(62,8 + 25,12 = 87,92 \, (\text{см}^2)\).
Ответ: \(87,92 \, \text{см}^2\).
Высота цилиндра равна ширине прямоугольника, который разворачивается в боковую поверхность цилиндра. Чтобы найти площадь боковой поверхности, нужно сначала определить длину этого прямоугольника. Длина прямоугольника равна длине окружности основания цилиндра, так как при разворачивании боковой поверхности цилиндра получается прямоугольник, одна сторона которого — высота цилиндра, а другая — длина окружности основания. Формула длины окружности: \(2 \pi r\), где \(r\) — радиус основания цилиндра. Подставляя значения, получаем: \(2 \cdot 3{,}14 \cdot 2 = 12{,}56\) см.
Далее рассчитываем площадь боковой поверхности, умножая высоту цилиндра на длину окружности основания. Высота равна 5 см, длина окружности — 12,56 см, значит площадь боковой поверхности равна \(5 \cdot 12{,}56 = 62{,}8\) см². Это площадь прямоугольника, который образует боковую поверхность цилиндра.
Теперь нужно вычислить площадь двух оснований цилиндра, которые представляют собой два круга с радиусом 2 см. Площадь одного круга вычисляется по формуле \( \pi r^2 \). Площадь двух оснований будет равна \(2 \pi r^2\). Подставляя значения, получаем: \(2 \cdot 3{,}14 \cdot 2^2 = 2 \cdot 3{,}14 \cdot 4 = 25{,}12\) см². Суммируя площадь боковой поверхности и площадь двух оснований, получаем полную площадь поверхности цилиндра: \(62{,}8 + 25{,}12 = 87{,}92\) см².
Ответ: \(87{,}92\) см².

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!