
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 225 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
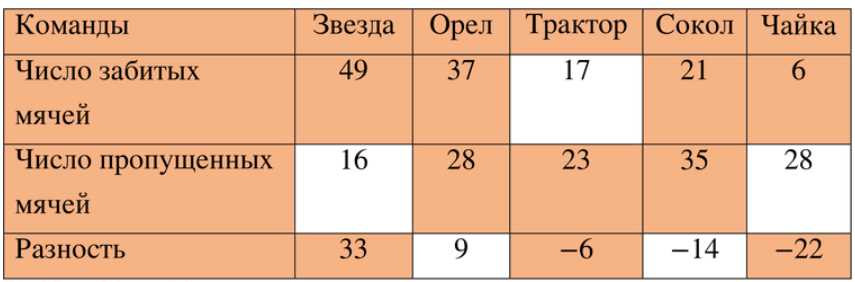
Заполните пустые места таблицы:
| Команды | «Звезда» | «Орёл» | «Трактор» | «Сокол» | «Чайка» |
| Число забитых мячей | 49 | 37 | 21 | 6 | |
| Число пропущенных мячей | 28 | 23 | 35 | ||
| Разность | 33 | −6 | −22 |
1) \(49-33=16\). Разность равна \(33\), значит пропущено \(49-33=16\) мячей.
2) \(37-28=9\). Разность равна \(9\), так как \(37-28=9\).
3) \(17-23=-6\). Разность равна \(-6\), так как \(17-23=-6\).
4) \(21-35=-14\). Разность равна \(-14\), так как \(21-35=-14\).
5) \(6-(-22)=28\). Пропущено \(28\) мячей, так как \(6-(-22)=6+22=28\).
1) В таблице для «Звезды» известны забитые мячи \(49\) и разность \(33\). Разность в таких задачах понимается как \( \text{забитые} — \text{пропущенные} \), то есть \(49-\text{пропущенные}=33\).
Чтобы найти пропущенные, переносим разность в правую часть: \(49-33=\text{пропущенные}\). Получаем \(49-33=16\), значит «Звезда» пропустила \(16\) мячей.
2) Для «Орла» в таблице даны забитые \(37\) и пропущенные \(28\). Разность находится вычитанием пропущенных из забитых, потому что сравниваем, на сколько забитых больше (или меньше), чем пропущенных: \( \text{разность}=37-28\).
Вычисляем: \(37-28=9\). Значит разность для «Орла» равна \(9\), что и соответствует заполненной строке «Разность».
3) Для «Трактора» в таблице указаны забитые \(17\) и пропущенные \(23\). Разность считается так же: \( \text{разность}=17-23\), потому что это \( \text{забитые} — \text{пропущенные} \).
Так как пропущенных больше, результат получается отрицательным: \(17-23=-6\). Следовательно, разность равна \(-6\), как в таблице.
4) Для «Сокола» даны забитые \(21\) и пропущенные \(35\). По определению разности считаем \( \text{разность}=21-35\), то есть от забитых отнимаем пропущенные.
Поскольку \(35>21\), разность отрицательная: \(21-35=-14\). Значит в строке «Разность» для «Сокола» стоит \(-14\).
5) Для «Чайки» известны забитые \(6\) и разность \(-22\). Используем ту же связь: \(6-\text{пропущенные}=-22\), потому что \( \text{забитые} — \text{пропущенные} = \text{разность}\).
Чтобы найти пропущенные, вычтем разность из забитых: \(\text{пропущенные}=6-(-22)\). Тогда \(6-(-22)=6+22=28\), значит «Чайка» пропустила \(28\) мячей.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!