
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 222 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
Отметьте на координатной прямой точки \(A(-4)\) и \(B(9)\). Найдите расстояние между точками \(A\) и \(B\) в единичных отрезках.
Отметим точки \(A(-4)\) и \(B(9)\) на координатной прямой.
Расстояние между ними равно: \(9-(-4)=9+4=13\) (единичных отрезков).
На координатной прямой точка \(A\) имеет координату \(-4\), а точка \(B\) — координату \(9\). Это значит, что \(A\) расположена левее нуля на 4 единицы, а \(B\) правее нуля на 9 единиц, поэтому отрезок между ними проходит через \(0\).
Расстояние между двумя точками на координатной прямой равно разности большей координаты и меньшей: нужно взять правую точку и вычесть левую. Здесь правая координата \(9\), левая \(-4\), поэтому получаем \(9-(-4)\).
При вычитании отрицательного числа знак меняется на плюс: \(9-(-4)=9+4\). Это отражает то, что расстояние состоит из двух частей: от \(-4\) до \(0\) это \(4\) единицы и от \(0\) до \(9\) это \(9\) единиц, вместе \(4+9\).
Следовательно, \(9+4=13\), значит расстояние между точками \(A\) и \(B\) равно \(13\) единичным отрезкам.



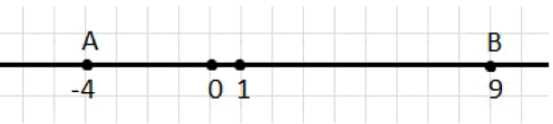



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!