
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 149 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
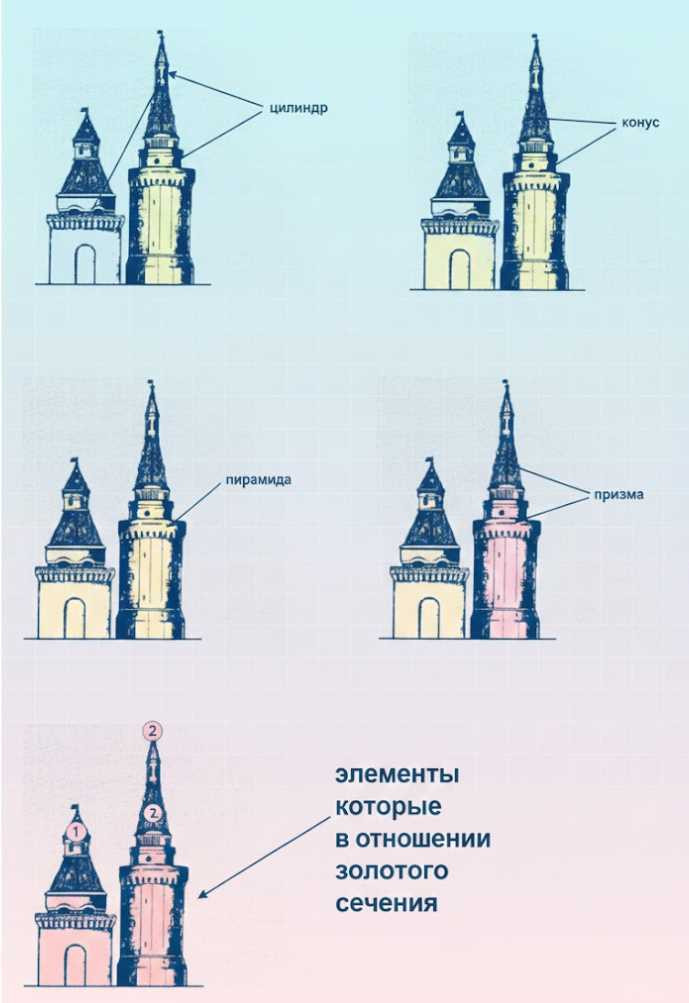
На рисунке показаны две башни Московского Кремля — Арсенальная и Тайницкая. Рассмотрите форму отдельных их частей: использованы ли архитекторами известные вам фигуры — призма, цилиндр, пирамида, конус? Проверьте, нет ли элементов, размеры которых находятся в отношении золотого сечения.
Архитекторами использованы фигуры для частей:
Арсенальная башня: основание – цилиндр, далее – пирамида, верх – конус.
Тайницкая башня: основание – призма, далее – пирамида, верх – конус.
Если визуально разделим башни на отрезки, то отношение основания башен к их верху будет равно золотому сечению.
Архитекторами для создания частей башен использованы простые геометрические фигуры, что позволяет легко представить форму и структуру каждой башни. Для Арсенальной башни основанием служит цилиндр, который представляет собой тело с круглыми основаниями и прямыми боковыми поверхностями. Над цилиндром расположена пирамида — многогранник с треугольными боковыми гранями, сходящимися в одной вершине. Верхняя часть башни выполнена в форме конуса, который плавно сужается к вершине, придавая башне характерную остроконечную форму.
Для Тайницкой башни основание выполнено в виде призмы — многогранника с двумя параллельными многоугольными основаниями и прямыми боковыми гранями. Далее, аналогично Арсенальной башне, идет пирамида, а верхняя часть также представляет собой конус. Такое сочетание фигур позволяет архитекторам создавать сложные и гармоничные формы башен, сочетая простоту и изящество.
Если визуально разделить башни на отдельные отрезки, то отношение длины основания башен к длине их верхней части равно золотому сечению. Золотое сечение — это иррациональное число, выражаемое формулой \( \varphi = \frac{1 + \sqrt{5}}{2} \approx 1{,}618 \). Это означает, что если длину основания башни обозначить за \( a \), а длину верхней части за \( b \), то выполняется равенство \( \frac{a}{b} = \varphi \). Такое соотношение придает башням эстетическую гармонию и пропорциональность, которые часто встречаются в природе и классической архитектуре.







Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!