
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 134 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
На координатной прямой отмечены числа \(a\) и \(a+1\) (рис. 31). Изобразите на этой же прямой числа \(a+2\); \(a+(−3)\); \(a+(−4,5)\); \(a+\left(−\frac{1}{2}\right)\).
На координатной прямой уже отмечены точки \(a\) и \(a+1\).
\(a+2\) находится правее \(a+1\), на расстоянии 1 единицы.
\(a+(-3) = a-3\) находится слева от \(a\), на 3 единицы.
\(a+(-4,5) = a-4,5\) находится еще левее, на 4,5 единицы от \(a\).
\(a+\left(-\frac{1}{2}\right) = a-\frac{1}{2}\) находится между \(a\) и \(a-1\), ближе к \(a\), на половину единицы слева.
На координатной прямой уже отмечены точки \(a\) и \(a+1\). Это означает, что точка \(a+1\) находится на расстоянии одной единицы вправо от точки \(a\). Чтобы изобразить числа, указанные в задании, нужно понимать их относительное расположение по отношению к \(a\).
Число \(a+2\) находится правее точки \(a+1\), так как \(2 > 1\). Расстояние между \(a+1\) и \(a+2\) равно одной единице, поэтому точка \(a+2\) будет расположена на координатной прямой на 2 единицы вправо от \(a\). Таким образом, \(a+2\) — это точка, смещённая на две единицы вправо от \(a\).
Числа с отрицательными слагаемыми, такие как \(a+(-3)\), \(a+(-4,5)\) и \(a+\left(-\frac{1}{2}\right)\), расположены слева от точки \(a\), так как отрицательное число сдвигает точку влево. Точка \(a+(-3) = a-3\) находится на 3 единицы левее \(a\), то есть на три шага влево. Аналогично, \(a+(-4,5) = a-4,5\) расположена ещё левее, на 4,5 единицы от \(a\). Точка \(a+\left(-\frac{1}{2}\right) = a-\frac{1}{2}\) находится ближе к \(a\), всего на половину единицы слева. Она расположена между \(a\) и \(a-1\), но ближе к \(a\).
Таким образом, все точки можно изобразить на координатной прямой, учитывая их смещение относительно точки \(a\): вправо для положительных слагаемых и влево для отрицательных, с точным расстоянием, равным абсолютному значению прибавляемого числа.



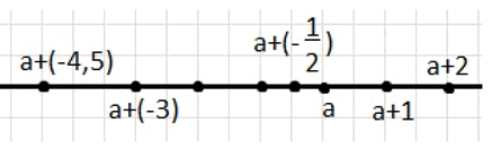



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!