ГДЗ по Математике 6 Класс Часть 2 Номер 131 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

Найдите с помощью координатной прямой сумму чисел:

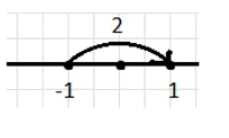
а) −1 и 2;

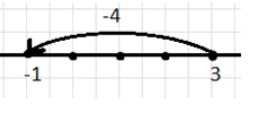
б) 3 и −4;

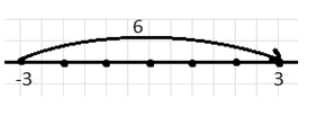
в) −3 и 6;

г) 1 и −5;

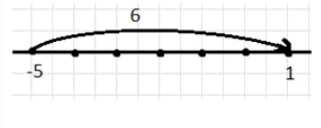
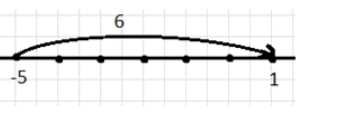
д) −5 и 6;

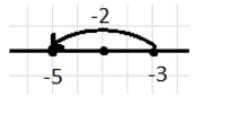
е) −3 и −2;

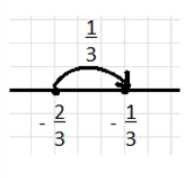
ж) \(-\frac{2}{3}\) и \(\frac{1}{3}\);

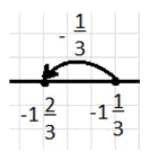
з) \(-1\frac{1}{3}\) и \(-\frac{1}{3}\).

а) \( -1 + 2 = 1 \)
Начинаем с -1, прибавляем 2, получаем 1.

б) \( 3 + (-4) = -1 \)
От 3 идём влево на 4, получаем -1.

в) \( -3 + 6 = 3 \)
От -3 идём вправо на 6, получаем 3.

г) \( 1 + (-5) = -4 \)
От 1 идём влево на 5, получаем -4.

д) \( -5 + 6 = 1 \)
От -5 идём вправо на 6, получаем 1.

е) \( -3 + (-2) = -5 \)
От -3 идём влево на 2, получаем -5.

ж) \( -\frac{2}{3} + \frac{1}{3} = -\frac{1}{3} \)
От -\(\frac{2}{3}\) идём вправо на \(\frac{1}{3}\), получаем -\(\frac{1}{3}\).

з) \( -1\frac{1}{3} + \left(-\frac{1}{3}\right) = -1\frac{2}{3} \)
От -\(1\frac{1}{3}\) идём влево на \(\frac{1}{3}\), получаем -\(1\frac{2}{3}\).

а) Рассмотрим выражение \( -1 + 2 = 1 \). Начинаем на числовой оси с точки \(-1\). Прибавление числа 2 означает движение вправо на 2 единицы. Если от \(-1\) сдвинуться вправо на 2, то попадём в точку \(1\). Это и есть результат сложения. Таким образом, \( -1 + 2 = 1 \).

При сложении положительного и отрицательного числа важно помнить, что положительное число сдвигает вправо, а отрицательное — влево. Здесь мы двигаемся вправо, поэтому итоговое значение увеличивается.

Такой подход помогает визуализировать арифметические операции и лучше понимать, как меняется положение на числовой оси при сложении.

б) В выражении \( 3 + (-4) = -1 \) начинаем с точки 3 на числовой оси. Прибавление числа \(-4\) означает движение влево на 4 единицы, так как число отрицательное. От 3 идём влево на 4, что приводит нас к точке \(-1\).

Это иллюстрирует правило сложения отрицательных чисел: прибавление отрицательного эквивалентно вычитанию. Таким образом, \( 3 + (-4) \) равно \( 3 — 4 \), что даёт \(-1\).

Визуализация на числовой оси помогает понять, что при прибавлении отрицательного числа мы фактически движемся назад по оси.

в) В случае \( -3 + 6 = 3 \) стартуем с точки \(-3\). Прибавление 6 означает движение вправо на 6 единиц. От \(-3\) идём вправо на 6, достигая точки \(3\).

Это показывает, что прибавление положительного числа увеличивает значение, смещая точку вправо. Здесь отрицательное число \(-3\) компенсируется большим положительным числом 6, в результате чего итог положительный.

Такое движение по оси помогает наглядно понять, как меняется сумма при разных знаках слагаемых.

г) Рассмотрим \( 1 + (-5) = -4 \). Начинаем с точки 1. Прибавление \(-5\) означает движение влево на 5 единиц. От 1 идём влево на 5, приходя к точке \(-4\).

Это пример того, как прибавление отрицательного числа уменьшает значение, смещая точку влево. В итоге сумма становится отрицательной, несмотря на положительное первое слагаемое.

Визуализация на числовой оси помогает понять, что прибавление отрицательного числа — это движение назад.

д) В выражении \( -5 + 6 = 1 \) стартуем с \(-5\). Прибавляем 6, то есть движемся вправо на 6 единиц. От \(-5\) идём вправо на 6, получая \(1\).

Это показывает, что положительное число может компенсировать отрицательное, смещая итог вправо. Сумма становится положительной, так как 6 больше по модулю, чем \(-5\).

Числовая ось наглядно демонстрирует, как сумма меняется в зависимости от величин и знаков слагаемых.

е) Для \( -3 + (-2) = -5 \) начинаем с \(-3\). Прибавление \(-2\) означает движение влево на 2. От \(-3\) идём влево на 2, достигая \(-5\).

Это пример сложения двух отрицательных чисел, где сумма становится ещё меньше (более отрицательной). Движение по оси влево показывает уменьшение значения.

Такой способ помогает понять, что при сложении отрицательных чисел итоговое значение уменьшается.

ж) В выражении \( -\frac{2}{3} + \frac{1}{3} = -\frac{1}{3} \) стартуем с точки \(-\frac{2}{3}\). Прибавляем \(\frac{1}{3}\), то есть движемся вправо на \(\frac{1}{3}\). От \(-\frac{2}{3}\) сдвигаемся вправо на \(\frac{1}{3}\), получая \(-\frac{1}{3}\).

Это показывает, как при сложении дробей с разными знаками результат зависит от величины слагаемых. Здесь положительная дробь частично компенсирует отрицательную.

Визуализация дробей на числовой оси помогает понять операцию сложения дробных чисел.

з) Рассмотрим \( -1\frac{1}{3} + \left(-\frac{1}{3}\right) = -1\frac{2}{3} \). Начинаем с точки \(-1\frac{1}{3}\). Прибавление \(-\frac{1}{3}\) означает движение влево на \(\frac{1}{3}\). От \(-1\frac{1}{3}\) идём влево на \(\frac{1}{3}\), получая \(-1\frac{2}{3}\).

Это пример сложения смешанного числа и отрицательной дроби. Итоговое значение уменьшается, так как прибавляется отрицательное число.

Использование числовой оси помогает наглядно увидеть, как меняется сумма при сложении смешанных чисел и дробей с разными знаками.