
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 128 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
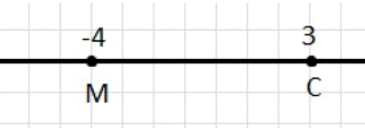
Отметьте на координатной прямой точку \(M(-4)\). После перемещения по координатной прямой она попала в точку \(C(3)\). Чему равно перемещение?
Перемещение равно: \(3 — (-4) = 7\).
На числовой прямой даны две точки: \(M\) с координатой \(-4\) и \(C\) с координатой \(3\). Чтобы найти перемещение, нужно определить, на сколько единиц точка \(C\) сместилась относительно точки \(M\). Перемещение — это разность координат конечной и начальной точек, то есть координаты \(C\) минус координаты \(M\).
В данном случае перемещение вычисляется по формуле \(3 — (-4)\). Обратите внимание, что знак минус перед \(-4\) меняет знак числа, превращая вычитание отрицательного числа в сложение. Это значит, что \(3 — (-4)\) эквивалентно \(3 + 4\). Таким образом, мы складываем 3 и 4, получая 7. Это показывает, что точка \(C\) находится на 7 единиц правее точки \(M\).
Итоговое перемещение равно \(7\). Это значение показывает, насколько далеко точка \(C\) сместилась вправо по числовой прямой относительно точки \(M\). Такой способ вычисления перемещения помогает точно определить расстояние между двумя точками на прямой, учитывая направление движения.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!