ГДЗ по Математике 6 Класс Часть 2 Номер 120 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

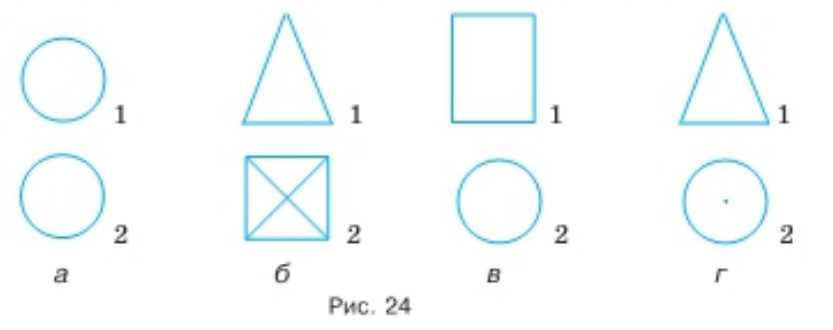
На рисунке 24 под цифрой 1 показан вид фигуры спереди, а под цифрой 2 — вид сверху. Какая это может быть фигура?

а) шар — тело, все точки поверхности которого равноудалены от центра.

б) четырехугольная пирамида — многогранник с четырёхугольником в основании и вершиной, соединённой с вершинами основания.

в) цилиндр — тело, образованное вращением прямоугольника вокруг одной из его сторон.

г) конус — тело, образованное вращением прямоугольного треугольника вокруг одного из катетов.

а) Шар — это трёхмерное геометрическое тело, все точки поверхности которого находятся на одинаковом расстоянии от центра. Это расстояние называется радиусом \(r\). Формально, шар можно определить как множество точек, удовлетворяющих условию \(x^2 + y^2 + z^2 = r^2\), где \(x, y, z\) — координаты точки в пространстве. Шар обладает полной симметрией относительно своего центра, что делает его важным объектом в геометрии и физике.

Поверхность шара называется сферой. Объём шара вычисляется по формуле \(V = \frac{4}{3} \pi r^3\), а площадь поверхности — по формуле \(S = 4 \pi r^2\). Эти формулы показывают, как объём и площадь зависят от радиуса. Шар широко используется в различных областях, от архитектуры до астрономии, благодаря своей уникальной форме и свойствам.

Кроме того, шар является примером тела вращения, которое можно получить вращением круга вокруг его диаметра. Это делает шар важным объектом для изучения в задачах механики и динамики, где симметрия и равномерность распределения массы играют ключевую роль.

б) Четырёхугольная пирамида — это многогранник, у которого основание представляет собой четырёхугольник, а остальные грани — треугольники, сходящиеся в одной вершине, называемой вершиной пирамиды. Основание может быть любым четырёхугольником: квадратом, прямоугольником, ромбом или произвольным четырёхугольником.

Пирамида характеризуется высотой \(h\), которая опускается из вершины перпендикулярно к плоскости основания. Объём пирамиды вычисляется по формуле \(V = \frac{1}{3} S_{осн} h\), где \(S_{осн}\) — площадь основания. Эта формула отражает, что объём пирамиды равен трети произведения площади основания на высоту.

Четырёхугольные пирамиды часто используются в архитектуре и инженерии, так как они обладают устойчивой конструкцией и интересными геометрическими свойствами. В частности, пирамида является примером усечённого конуса с плоским основанием и вершиной.

в) Цилиндр — это тело, образованное вращением прямоугольника вокруг одной из его сторон, которая становится осью цилиндра. В результате получается поверхность, состоящая из двух параллельных кругов (оснований) и боковой поверхности, которая является частью боковой поверхности конуса.

Основные параметры цилиндра — радиус основания \(r\) и высота \(h\). Объём цилиндра вычисляется по формуле \(V = \pi r^2 h\), которая показывает, что объём равен произведению площади основания на высоту. Площадь боковой поверхности равна \(S_{бок} = 2 \pi r h\), а полная площадь поверхности — \(S = 2 \pi r (r + h)\).

Цилиндры широко применяются в технике и повседневной жизни, например, в строительстве, машиностроении и упаковке, благодаря простоте формы и удобству использования.

г) Конус — это тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов, который становится осью конуса. В результате получается фигура с круглым основанием и вершиной, расположенной на оси вращения.

Основные параметры конуса — радиус основания \(r\) и высота \(h\). Объём конуса вычисляется по формуле \(V = \frac{1}{3} \pi r^2 h\), что аналогично формуле объёма пирамиды, так как конус можно рассматривать как пирамиду с бесконечным числом граней. Площадь боковой поверхности конуса равна \(S_{бок} = \pi r l\), где \(l\) — образующая конуса, вычисляемая по теореме Пифагора как \(l = \sqrt{r^2 + h^2}\).

Конусы применяются в различных областях — от архитектуры до производства деталей машин, и обладают важными свойствами, связанными с их формой и симметрией.