ГДЗ по Математике 6 Класс Часть 2 Номер 115 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

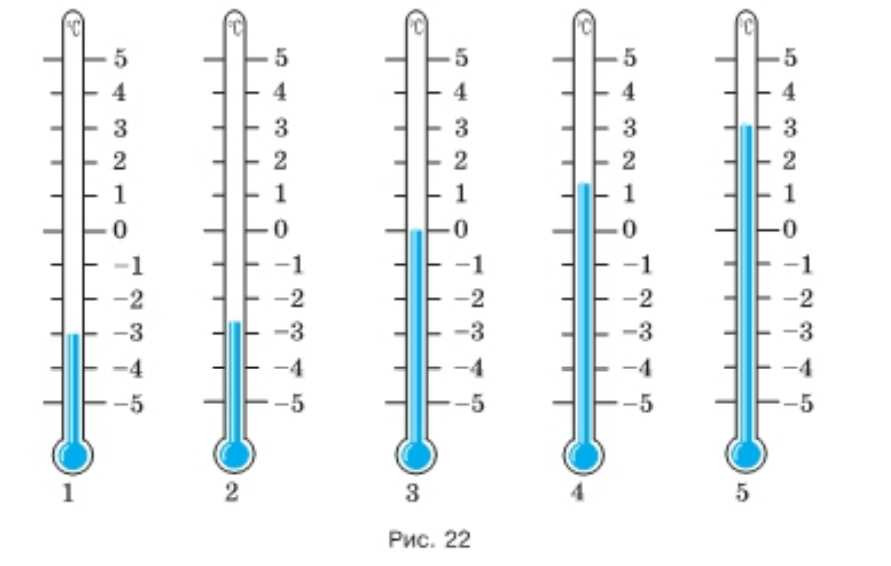
Прочитайте показания термометров, изображённых на рисунке 22. Какую температуру будет показывать каждый из этих термометров, если температура изменится:

а) на \(-1^{\circ}\!C\);

б) на \(1^{\circ}\!C\);

в) на \(2^{\circ}\!C\);

г) на \(-2^{\circ}\!C\)?

1) Было \( -3^\circ C\), стало: \(T=-3+\Delta T\).
а) \( -3+(-1)=-4^\circ C\)
б) \( -3+1=-2^\circ C\)
в) \( -3+2=-1^\circ C\)
г) \( -3+(-2)=-5^\circ C\)

2) Было \( -2{,}7^\circ C\), стало: \(T=-2{,}7+\Delta T\).
а) \( -2{,}7+(-1)=-3{,}7^\circ C\)
б) \( -2{,}7+1=-1{,}7^\circ C\)
в) \( -2{,}7+2=-0{,}7^\circ C\)
г) \( -2{,}7+(-2)=-4{,}7^\circ C\)

3) Было \(0^\circ C\), стало: \(T=0+\Delta T\).
а) \(0+(-1)=-1^\circ C\)
б) \(0+1=1^\circ C\)
в) \(0+2=2^\circ C\)
г) \(0+(-2)=-2^\circ C\)

4) Было \(1{,}3^\circ C\), стало: \(T=1{,}3+\Delta T\).
а) \(1{,}3+(-1)=0{,}3^\circ C\)
б) \(1{,}3+1=2{,}3^\circ C\)
в) \(1{,}3+2=3{,}3^\circ C\)
г) \(1{,}3+(-2)=-0{,}7^\circ C\)

5) Было \(3^\circ C\), стало: \(T=3+\Delta T\).
а) \(3+(-1)=2^\circ C\)
б) \(3+1=4^\circ C\)
в) \(3+2=5^\circ C\)
г) \(3+(-2)=1^\circ C\)

1) На первом термометре показано \( -3^\circ C\). Изменение температуры учитываем сложением: новая температура \(T_{\text{нов}}=T_{\text{нач}}+\Delta T\), то есть \(T_{\text{нов}}=-3+\Delta T\). Знак \(\Delta T\) важен: если \(\Delta T<0\), температура понижается (число становится «более отрицательным»), если \(\Delta T>0\), температура повышается (число растёт).

а) При изменении на \(-1^\circ C\): \(T=-3+(-1)=-4^\circ C\). Это означает, что стало холоднее на \(1^\circ C\), поэтому показание ушло на один градус ниже.
б) При изменении на \(1^\circ C\): \(T=-3+1=-2^\circ C\). Температура повысилась на \(1^\circ C\), поэтому отрицательное значение стало ближе к нулю.
в) При изменении на \(2^\circ C\): \(T=-3+2=-1^\circ C\). Повышение на \(2^\circ C\) сдвигает показание на два деления вверх.
г) При изменении на \(-2^\circ C\): \(T=-3+(-2)=-5^\circ C\). Понижение на \(2^\circ C\) делает значение ещё ниже, то есть более отрицательным.

2) На втором термометре показано \( -2{,}7^\circ C\). Правило то же: \(T_{\text{нов}}=-2{,}7+\Delta T\). Здесь важно аккуратно работать с десятичной дробью: прибавляем или вычитаем целое число градусов, сохраняя десятичную часть \(0{,}7\).

а) При изменении на \(-1^\circ C\): \(T=-2{,}7+(-1)=-3{,}7^\circ C\). Понижение на один градус делает число на \(1\) меньше.
б) При изменении на \(1^\circ C\): \(T=-2{,}7+1=-1{,}7^\circ C\). Повышение на один градус приближает температуру к нулю на \(1^\circ C\).
в) При изменении на \(2^\circ C\): \(T=-2{,}7+2=-0{,}7^\circ C\). Повышение на два градуса даёт значение, которое всё ещё отрицательное, но намного ближе к нулю.
г) При изменении на \(-2^\circ C\): \(T=-2{,}7+(-2)=-4{,}7^\circ C\). Понижение на два градуса отнимает \(2\) и делает температуру заметно ниже.

3) На третьем термометре показано \(0^\circ C\). Здесь удобно видеть, что \(0\) — точка отсчёта: \(T_{\text{нов}}=0+\Delta T=\Delta T\). То есть новое показание просто равно величине изменения, с тем же знаком.

а) При изменении на \(-1^\circ C\): \(T=0+(-1)=-1^\circ C\). Температура стала отрицательной, значит опустилась ниже нуля.
б) При изменении на \(1^\circ C\): \(T=0+1=1^\circ C\). Температура стала положительной, значит поднялась выше нуля.
в) При изменении на \(2^\circ C\): \(T=0+2=2^\circ C\). Подъём на \(2^\circ C\) даёт два градуса тепла.
г) При изменении на \(-2^\circ C\): \(T=0+(-2)=-2^\circ C\). Понижение на \(2^\circ C\) даёт два градуса мороза.

4) На четвёртом термометре показано \(1{,}3^\circ C\). Применяем ту же формулу: \(T_{\text{нов}}=1{,}3+\Delta T\). Прибавление положительного числа увеличивает показание, прибавление отрицательного уменьшает; при уменьшении на \(2^\circ C\) температура может перейти через ноль и стать отрицательной.

а) При изменении на \(-1^\circ C\): \(T=1{,}3+(-1)=0{,}3^\circ C\). Стало прохладнее на один градус, но температура остаётся выше нуля.
б) При изменении на \(1^\circ C\): \(T=1{,}3+1=2{,}3^\circ C\). Стало теплее на один градус, десятичная часть сохраняется.
в) При изменении на \(2^\circ C\): \(T=1{,}3+2=3{,}3^\circ C\). Повышение на два градуса увеличивает целую часть на \(2\).
г) При изменении на \(-2^\circ C\): \(T=1{,}3+(-2)=-0{,}7^\circ C\). Понижение на два градуса «перешагивает» через \(0^\circ C\), поэтому результат отрицательный.

5) На пятом термометре показано \(3^\circ C\). Новое значение считаем по \(T_{\text{нов}}=3+\Delta T\). Здесь все изменения целые, поэтому достаточно обычного сложения и вычитания: повышение увеличивает число, понижение уменьшает.

а) При изменении на \(-1^\circ C\): \(T=3+(-1)=2^\circ C\). Стало холоднее на один градус, показание уменьшилось на \(1\).
б) При изменении на \(1^\circ C\): \(T=3+1=4^\circ C\). Стало теплее на один градус, показание увеличилось на \(1\).
в) При изменении на \(2^\circ C\): \(T=3+2=5^\circ C\). Стало теплее на два градуса, поэтому прибавили \(2\).
г) При изменении на \(-2^\circ C\): \(T=3+(-2)=1^\circ C\). Стало холоднее на два градуса, поэтому вычли \(2\).