ГДЗ по Математике 6 Класс Часть 2 Номер 11 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

Изобразите точкой на координатной прямой число \(a\), если:

а) \(a=-6;\ +3;\ -5;\ -8;\ +10;\ +9;\ +7;\ -7\);

б) \(a=2;\ -1;\ 3;\ -5;\ 4;\ \frac{7}{8};\ -\frac{5}{6}\).

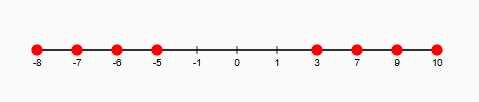
а) Точки на числовой прямой соответствуют значениям:
\(-8, -7, -6, -5, -1, 0, 1, 3, 7, 9, 10\).
Отметим точки для \(a\):
\(-6, +3, -5, -8, +10, +9, +7, -7\).

б) Точки на числовой прямой соответствуют значениям:
\(-1, 0, 1, 2, 3, 4\), а также дробным \(\frac{7}{8}\) и \(-\frac{5}{6}\), которые расположены между 0 и 1, и между -1 и 0 соответственно.
Отметим точки для \(a\):
\(2, -1, 3, -5, 4, \frac{7}{8}, -\frac{5}{6}\).

а) Рассмотрим множество чисел \(a = -6; +3; -5; -8; +10; +9; +7; -7\). Каждое из этих чисел нужно отобразить на числовой оси. На оси уже отмечены целые числа: \(-8, -7, -6, -5, -1, 0, 1, 3, 7, 9, 10\). Для каждого значения \(a\) найдём соответствующее место на оси и отметим точкой. Например, число \(-6\) находится между \(-7\) и \(-5\), точка для \(+3\) уже отмечена, так как на оси есть отметка \(3\). Аналогично отметим все остальные числа из списка: \(-5, -8, +10, +9, +7, -7\). Таким образом, каждое число из множества \(a\) соответствует одной точке на оси, что визуально подтверждает правильность их расположения.

б) Теперь рассмотрим другое множество чисел: \(a = 2; -1; 3; -5; 4; \frac{7}{8}; -\frac{5}{6}\). Здесь есть как целые числа, так и дробные. Целые числа \(2, -1, 3, -5, 4\) легко отметить на числовой оси, так как они соответствуют уже отмеченным точкам. Дробные числа \(\frac{7}{8}\) и \(-\frac{5}{6}\) расположены между целыми числами: \(\frac{7}{8}\) находится между 0 и 1, ближе к 1, а \(-\frac{5}{6}\) — между -1 и 0, ближе к -1. Для точного отображения дробных значений на оси нужно представить их как доли от единицы и отметить соответствующие точки с учётом этой пропорции.

Важно понимать, что числовая ось — это непрерывная линия, на которой каждое число, будь то целое или дробное, занимает своё уникальное положение. Отмечая точки для заданных чисел, мы визуализируем их относительное расположение и порядок. Целые числа занимают фиксированные позиции, а дробные числа располагаются между ними в зависимости от величины дроби. Таким образом, на числовой оси можно наглядно видеть, какие числа больше или меньше других, и где именно они находятся относительно нуля и друг друга.