ГДЗ по Математике 6 Класс Часть 2 Номер 102 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

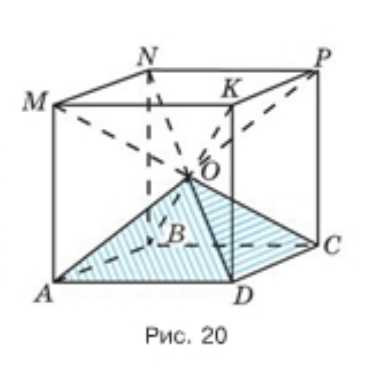
Из рисунка 20 видно, что куб можно составить из шести одинаковых четырёхугольных пирамид, у которых вершина \(O\), а основаниями служат грани куба. Найдите объём пирамиды, если ребро куба 1,2 см. Найдите ребро куба, если объём одной пирамиды \(\frac{1}{6}\ \text{см}^3\).

Вычислим объём куба с ребром \(1,2\) см: \(V_{\text{куба}}=(1,2)^3=1,728\ \text{см}^3\).

Значит, объём пирамиды равен: \(V_{\text{пирамиды}}=\frac{1,728}{6}=0,288\ \text{см}^3\).

Если объём одной пирамиды \(\frac{1}{6}\ \text{см}^3\), то объём куба равен: \(V_{\text{куба}}=6\cdot V_{\text{пирамиды}}=6\cdot \frac{1}{6}=1\ \text{см}^3\).

Тогда ребро куба равно: \(a^3=1\), \(a=1\ \text{см}\).

Ответ: \(0,288\ \text{см}^3;\ 1\ \text{см}\).

Вычислим объём куба с ребром \(1,2\) см по формуле объёма куба \(V_{\text{куба}}=a^3\). Подставляем \(a=1,2\): \(V_{\text{куба}}=(1,2)^3\). Возводим в третью степень: \(1,2\cdot 1,2\cdot 1,2=1,44\cdot 1,2=1,728\), значит \(V_{\text{куба}}=1,728\ \text{см}^3\).

По условию (как в решении на фото) объём пирамиды составляет \(\frac{1}{6}\) объёма куба, то есть из объёма куба можно получить объём одной пирамиды делением на \(6\). Поэтому \(V_{\text{пирамиды}}=\frac{V_{\text{куба}}}{6}=\frac{1,728}{6}=0,288\ \text{см}^3\). Деление выполнено напрямую: \(1,728:6=0,288\).

Во второй части используем обратную связь: если объём одной пирамиды равен \(\frac{1}{6}\ \text{см}^3\), то объём куба в \(6\) раз больше, потому что \(V_{\text{куба}}=6\cdot V_{\text{пирамиды}}\). Подставляем \(V_{\text{пирамиды}}=\frac{1}{6}\ \text{см}^3\): \(V_{\text{куба}}=6\cdot \frac{1}{6}=1\ \text{см}^3\).

Теперь найдём ребро куба \(a\), зная его объём: \(V_{\text{куба}}=a^3\). Так как \(V_{\text{куба}}=1\ \text{см}^3\), получаем \(a^3=1\). Единственное положительное значение ребра, удовлетворяющее этому, \(a=1\ \text{см}\), потому что \(1^3=1\).

Ответ: \(0,288\ \text{см}^3;\ 1\ \text{см}\).