ГДЗ по Математике 6 Класс Часть 2 Номер 10 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

 Отметьте на координатной прямой точку, имеющую координату \(x\), если \(x=-7;\ 3,3;\ -5,2;\ -1;\ 2;\ -1,8;\ \frac{5}{3};\ -\frac{7}{2}\).

\(x = -7; 3,3; -5,2; -1; 2; -1,8; \frac{5}{3} = 1 \frac{2}{3}; -\frac{7}{2} = -3,5\).

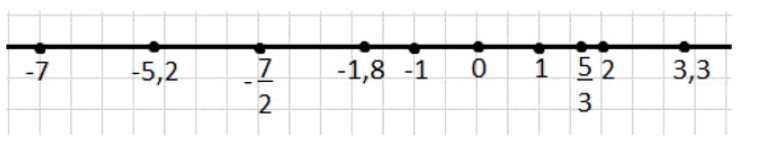
На координатной прямой отмечены точки с этими координатами:
— \(-7\) — слева,
— \(-5,2\) — чуть правее,
— \(-\frac{7}{2} = -3,5\) — между \(-5,2\) и \(-1,8\),
— \(-1,8\) — между \(-3,5\) и \(-1\),
— \(-1\),
— \(2\),
— \(\frac{5}{3} = 1 \frac{2}{3}\) — между \(1\) и \(2\),
— \(3,3\) — справа.

Рассмотрим каждое значение \(x\) и его расположение на координатной прямой. Координатная прямая — это числовая ось, на которой точки располагаются в порядке возрастания значений слева направо. Отрицательные числа находятся слева от нуля, а положительные — справа. Чтобы правильно отметить точки, нужно точно определить их числовое значение и расположить их в соответствующем месте.

Первое число — \(x = -7\). Это отрицательное число, расположенное далеко слева от нуля. На координатной прямой оно будет отмечено в точке, удалённой на 7 единиц влево от нуля. Следующее число — \(3,3\), это положительное число, чуть больше трёх, поэтому его отметка будет справа от нуля, между 3 и 4. Третье число — \( -5,2 \), также отрицательное, но ближе к нулю, чем \(-7\). Значит, точка с координатой \(-5,2\) будет расположена правее \(-7\), но левее нуля.

Далее идут числа \(-1\), \(2\), и \(-1,8\). Числа \(-1\) и \(-1,8\) отрицательные, но \(-1\) ближе к нулю, чем \(-1,8\), значит \(-1,8\) будет левее \(-1\). Число \(2\) положительное, поэтому точка с координатой \(2\) будет справа от нуля. Следующие числа — дроби: \(\frac{5}{3}\) и \(-\frac{7}{2}\). Число \(\frac{5}{3}\) — это неправильная дробь, равная \(1 \frac{2}{3}\), то есть примерно \(1,666\). Следовательно, точка с координатой \(\frac{5}{3}\) находится между \(1\) и \(2\), ближе к \(2\). Число \(-\frac{7}{2}\) равно \(-3,5\), то есть находится между \(-5,2\) и \(-1,8\), ближе к середине.

Таким образом, на координатной прямой точки будут расположены в следующем порядке слева направо: \( -7; -5,2; -\frac{7}{2} = -3,5; -1,8; -1; 0; \frac{5}{3} = 1 \frac{2}{3}; 2; 3,3 \). Каждая точка отмечена в соответствии с её числовым значением, что позволяет визуально оценить их взаимное расположение и расстояния между ними.