
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 887 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
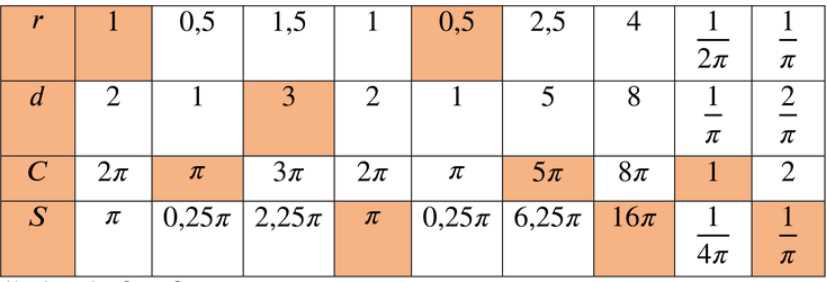
Заполните таблицу:
| \(r\) | 1 | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | 0,5 | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) |
| \(d\) | \(\emptyset\) | \(\emptyset\) | 3 | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) |
| \(C\) | \(\emptyset\) | \(\pi\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(5\pi\) | 1 | \(\emptyset\) |
| \(S\) | \(\emptyset\) | \(\emptyset\) | \(\emptyset\) | \(\pi\) | \(\emptyset\) | \(\emptyset\) | \(16\pi\) | \(\frac{1}{\pi}\) |
1) \( r = 1 \). Диаметр \( d = 2r = 2 \). Длина окружности \( C = \pi d = 2\pi \). Площадь \( S = \pi r^2 = \pi \).
2) \( C = \pi \). Диаметр \( d = \frac{C}{\pi} = 1 \). Радиус \( r = \frac{d}{2} = 0{,}5 \). Площадь \( S = \pi r^2 = 0{,}25\pi \).
3) \( d = 3 \). Радиус \( r = \frac{d}{2} = 1{,}5 \). Длина окружности \( C = \pi d = 3\pi \). Площадь \( S = \pi r^2 = 2{,}25\pi \).
4) \( S = \pi \). Радиус \( r = \sqrt{\frac{S}{\pi}} = 1 \). Диаметр \( d = 2r = 2 \). Длина окружности \( C = \pi d = 2\pi \).
5) \( r = 0{,}5 \). Диаметр \( d = 2r = 1 \). Длина окружности \( C = \pi d = \pi \). Площадь \( S = \pi r^2 = 0{,}25\pi \).
6) \( C = 5\pi \). Диаметр \( d = \frac{C}{\pi} = 5 \). Радиус \( r = \frac{d}{2} = 2{,}5 \). Площадь \( S = \pi r^2 = 6{,}25\pi \).
7) \( S = 16\pi \). Радиус \( r = \sqrt{\frac{S}{\pi}} = 4 \). Диаметр \( d = 2r = 8 \). Длина окружности \( C = \pi d = 8\pi \).
8) \( C = 1 \). Диаметр \( d = \frac{C}{\pi} = \frac{1}{\pi} \). Радиус \( r = \frac{d}{2} = \frac{1}{2\pi} \). Площадь \( S = \pi r^2 = \frac{1}{4\pi} \).
9) \( S = \frac{1}{\pi} \). Радиус \( r = \sqrt{\frac{S}{\pi}} = \frac{1}{\pi} \). Диаметр \( d = 2r = \frac{2}{\pi} \). Длина окружности \( C = \pi d = 2 \).
1) В первом примере нам даны длина радиуса \( r = 1 \). Сначала вычислим диаметр \( d \), который равен удвоенному радиусу, то есть \( d = 2 \cdot r = 2 \cdot 1 = 2 \). Далее найдем длину окружности \( C \), используя формулу \( C = \pi d \). Подставляя значение диаметра, получаем \( C = \pi \cdot 2 = 2\pi \). Затем вычислим площадь круга \( S \), которая равна \( S = \pi r^2 \). Подставляя \( r = 1 \), получаем \( S = \pi \cdot 1^2 = \pi \).
Во втором примере дана длина окружности \( C = \pi \). Из формулы длины окружности \( C = \pi d \) выразим диаметр: \( d = \frac{C}{\pi} = \frac{\pi}{\pi} = 1 \). Теперь найдем радиус \( r \), который равен половине диаметра: \( r = \frac{d}{2} = \frac{1}{2} = 0{,}5 \). Площадь круга вычисляется по формуле \( S = \pi r^2 \), подставляя \( r = 0{,}5 \), получаем \( S = \pi \cdot (0{,}5)^2 = \pi \cdot 0{,}25 = 0{,}25\pi \).
В третьем примере дан диаметр \( d = 3 \). Сначала найдем радиус \( r \), который равен половине диаметра: \( r = \frac{d}{2} = \frac{3}{2} = 1{,}5 \). Длина окружности вычисляется как \( C = \pi d = \pi \cdot 3 = 3\pi \). Площадь круга равна \( S = \pi r^2 \), подставляя \( r = 1{,}5 \), получаем \( S = \pi \cdot (1{,}5)^2 = \pi \cdot 2{,}25 = 2{,}25\pi \).
4) В этом случае дана площадь круга \( S = \pi \). Используя формулу площади \( S = \pi r^2 \), выразим радиус: \( r^2 = \frac{S}{\pi} = \frac{\pi}{\pi} = 1 \), откуда \( r = \sqrt{1} = 1 \). Диаметр равен удвоенному радиусу: \( d = 2r = 2 \cdot 1 = 2 \). Длина окружности рассчитывается по формуле \( C = \pi d \), подставляя \( d = 2 \), получаем \( C = \pi \cdot 2 = 2\pi \).
5) В пятом примере дан радиус \( r = 0{,}5 \). Сначала найдем диаметр: \( d = 2r = 2 \cdot 0{,}5 = 1 \). Длина окружности равна \( C = \pi d = \pi \cdot 1 = \pi \). Площадь круга вычисляется по формуле \( S = \pi r^2 \), подставляя \( r = 0{,}5 \), получаем \( S = \pi \cdot (0{,}5)^2 = \pi \cdot 0{,}25 = 0{,}25\pi \).
6) Здесь дана длина окружности \( C = 5\pi \). Выразим диаметр из формулы \( C = \pi d \): \( d = \frac{C}{\pi} = \frac{5\pi}{\pi} = 5 \). Радиус равен половине диаметра: \( r = \frac{d}{2} = \frac{5}{2} = 2{,}5 \). Площадь круга вычисляется по формуле \( S = \pi r^2 \), подставляя \( r = 2{,}5 \), получаем \( S = \pi \cdot (2{,}5)^2 = \pi \cdot 6{,}25 = 6{,}25\pi \).
7) В седьмом примере дана площадь круга \( S = 16\pi \). Выразим радиус из формулы площади: \( r^2 = \frac{S}{\pi} = \frac{16\pi}{\pi} = 16 \), откуда \( r = \sqrt{16} = 4 \). Диаметр равен \( d = 2r = 2 \cdot 4 = 8 \). Длина окружности равна \( C = \pi d = \pi \cdot 8 = 8\pi \).
8) Здесь дана длина окружности \( C = 1 \). Выразим диаметр из формулы \( C = \pi d \): \( d = \frac{C}{\pi} = \frac{1}{\pi} \). Радиус равен половине диаметра: \( r = \frac{d}{2} = \frac{1}{2\pi} \). Площадь круга вычисляется по формуле \( S = \pi r^2 \), подставляя \( r = \frac{1}{2\pi} \), получаем \( S = \pi \cdot \left(\frac{1}{2\pi}\right)^2 = \pi \cdot \frac{1}{4\pi^2} = \frac{1}{4\pi} \).
9) В последнем примере дана площадь круга \( S = \frac{1}{\pi} \). Выразим радиус из формулы площади: \( r^2 = \frac{S}{\pi} = \frac{\frac{1}{\pi}}{\pi} = \frac{1}{\pi^2} \), откуда \( r = \sqrt{\frac{1}{\pi^2}} = \frac{1}{\pi} \). Диаметр равен \( d = 2r = 2 \cdot \frac{1}{\pi} = \frac{2}{\pi} \). Длина окружности вычисляется по формуле \( C = \pi d = \pi \cdot \frac{2}{\pi} = 2 \).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!