ГДЗ по Математике 6 Класс Часть 1 Номер 863 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

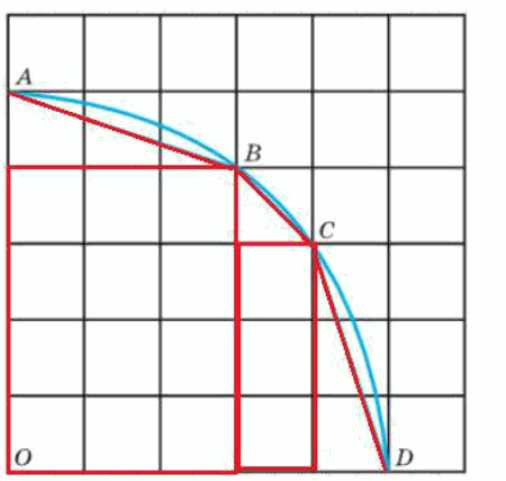
По рисунку 44 найдите площадь пятиугольника \(OABCD\). Сравните её с площадью четверти круга, радиус \(OD\) которого равен 5 см.

1) Так как радиус круга равен 5 см, то одна клетка равна 1 см.

2) Площадь пятиугольника \( OABCD \) равна сумме площадей двух прямоугольников (12 клеток и 3 клетки), двух прямоугольных треугольников, которые в сумме имеют 3 клетки, и еще половины клетки:
\( 15 + 3 + 0{,}5 = 18{,}5 \, (см^2) \).

3) Площадь четверти круга равна:
\( S = \frac{\pi r^2}{4} = \frac{3{,}14 \cdot 5^2}{4} = 0{,}785 \cdot 25 = 19{,}625 \, (см^2) \).

4) Следовательно, площадь пятиугольника меньше площади четверти круга, так как:
\( 18{,}5 < 19{,}625 \). Ответ: площадь четверти круга больше площади пятиугольника.

1) Радиус круга задан равным 5 см. На изображении видно, что круг вписан в квадрат, разбитый на клетки. Каждая клетка — это квадрат со стороной 1 см, так как весь квадрат имеет сторону 10 см (равную диаметру круга). Следовательно, площадь одной клетки равна \(1 \times 1 = 1 \, см^2\). Это важно, чтобы потом правильно посчитать площадь пятиугольника, используя количество клеток.

2) Пятиугольник \(OABCD\) разбит на несколько фигур, площадь которых легко вычислить, подсчитывая клетки. Сначала считаем площадь двух прямоугольников: первый занимает 12 клеток, второй — 3 клетки, итого \(12 + 3 = 15 \, см^2\). Далее идут два прямоугольных треугольника, которые вместе занимают 3 клетки. Плюс есть еще половина клетки, то есть \(0{,}5 \, см^2\). Складываем все части:
\(15 + 3 + 0{,}5 = 18{,}5 \, см^2\). Таким образом, площадь пятиугольника равна 18,5 квадратных сантиметров.

3) Теперь вычислим площадь четверти круга. Формула площади круга — \( \pi r^2 \), где \(r\) — радиус. Четверть круга — это четвертая часть полной площади, значит:
\( S = \frac{\pi r^2}{4} \). Подставляем значения:
\( r = 5 \, см \), \( \pi \approx 3{,}14 \), тогда
\( S = \frac{3{,}14 \times 5^2}{4} = \frac{3{,}14 \times 25}{4} = 0{,}785 \times 25 = 19{,}625 \, см^2 \).
Расчёт показывает, что площадь четверти круга равна 19,625 квадратных сантиметров.

4) Сравниваем площади пятиугольника и четверти круга. Площадь пятиугольника равна 18,5 см², а площадь четверти круга — 19,625 см². Очевидно, что
\( 18{,}5 < 19{,}625 \), значит площадь пятиугольника меньше площади четверти круга. 5) Вывод: площадь пятиугольника, ограниченного отрезками и дугами внутри квадрата, меньше площади соответствующей четверти круга с радиусом 5 см. Это подтверждается точным подсчётом клеток и вычислением площади круга по формуле. Таким образом, можно сделать заключение, что площадь фигуры, ограниченной дугой круга, больше, чем площадь пятиугольника, построенного внутри той же области.