ГДЗ по Математике 6 Класс Часть 1 Номер 843 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

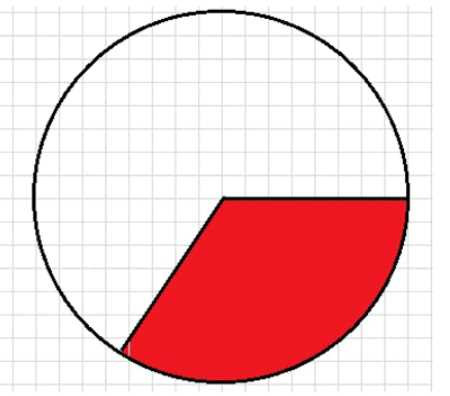
Начертите окружность и постройте два её радиуса, угол между которыми 120°. Закрасьте часть круга между этими радиусами. Какая часть круга окажется закрашенной и какая часть круга останется незакрашенной?

Выполним условия задачи:

\(120^\circ\) — закрашены красным цветом.

1) Весь круг равен \(360^\circ\).

Пусть \(x\) — закрашенная часть круга, а 1 — весь круг.

\(360^\circ = 1\)
\(120^\circ = x\)

Составим пропорцию:
\(\frac{120}{360} = \frac{x}{1}\)

\(x = \frac{120}{360} = \frac{12}{36} = \frac{1}{3}\) — часть круга закрашена.

2) Тогда незакрашенная часть круга равна:
\(1 — \frac{1}{3} = \frac{2}{3}\) (части).

Ответ: \(\frac{1}{3}\) часть; \(\frac{2}{3}\) части.

В задаче дан круг, который полностью равен \(360^\circ\). Из этого следует, что весь круг можно считать за единицу, то есть за 1. Это удобно для вычисления долей, которые занимают определённые части круга. В условии указано, что сектор, закрашенный красным цветом, равен \(120^\circ\). Нужно определить, какую часть всего круга занимает этот красный сектор.

Пусть \(x\) — это часть круга, которая закрашена красным. Тогда мы можем составить пропорцию, исходя из того, что весь круг — это 1, а весь круг в градусах — \(360^\circ\). Значит, если \(360^\circ\) соответствует 1, то \(120^\circ\) будет соответствовать \(x\). Запишем это в виде пропорции:
\(\frac{120}{360} = \frac{x}{1}\).
Решая это уравнение, получаем
\(x = \frac{120}{360} = \frac{12}{36} = \frac{1}{3}\).
Это означает, что красный сектор занимает ровно треть всей площади круга.

Теперь, чтобы найти долю незакрашенной части круга, нужно отнять долю закрашенной части от целого круга. Поскольку весь круг — это 1, а закрашенная часть — \(\frac{1}{3}\), то незакрашенная часть будет равна
\(1 — \frac{1}{3} = \frac{2}{3}\).
Таким образом, незакрашенная часть круга занимает две трети всего круга. Итоговый ответ: закрашенная часть — \(\frac{1}{3}\), незакрашенная часть — \(\frac{2}{3}\).