ГДЗ по Математике 6 Класс Часть 1 Номер 730 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

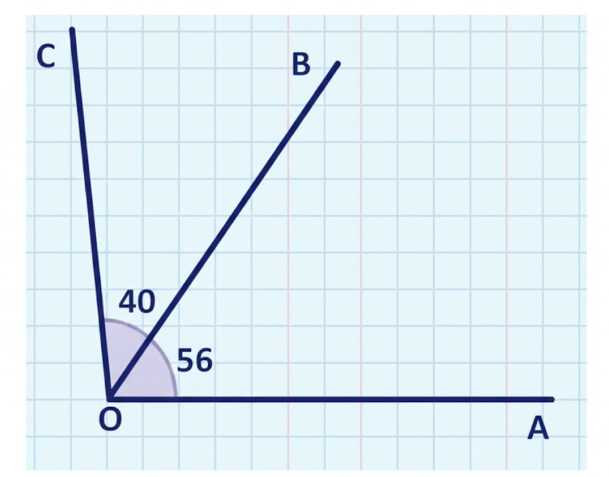
Внутри угла \(AOC\) проведён луч \(OB\) так, что \(\angle AOB=56^\circ\) и \(\angle BOC=40^\circ\). Какую часть угла \(AOC\) составляет угол \(AOB\); угол \(BOC\)? Выполните построение этих углов с помощью транспортира.

1) Найдем угол \( AOC \):
\( 56 + 40 = 96^\circ \).

2) Найдем, какую часть угла \( AOC \) составляет угол \( AOB \):
\( 56 : 96 = \frac{56}{96} = \frac{14}{24} = \frac{7}{12} \) (часть).

3) Найдем, какую часть угла \( AOC \) составляет угол \( BOC \):
\( 40 : 96 = \frac{40}{96} = \frac{10}{24} = \frac{5}{12} \) (часть).

1) Сначала найдем величину угла \( AOC \). Из условия известно, что угол \( AOC \) состоит из двух частей: угла \( AOB \), равного \( 56^\circ \), и угла \( BOC \), равного \( 40^\circ \). Чтобы найти общий угол \( AOC \), нужно сложить эти два угла. Выполним сложение: \( 56 + 40 = 96^\circ \). Таким образом, угол \( AOC \) равен \( 96^\circ \).

2) Теперь определим, какую часть от угла \( AOC \) составляет угол \( AOB \). Для этого нужно разделить величину угла \( AOB \) на величину угла \( AOC \). Выполним деление: \( 56 : 96 \). Запишем это в виде дроби: \( \frac{56}{96} \). Чтобы упростить дробь, найдем общий делитель числителя и знаменателя, это 8. Разделим числитель и знаменатель на 8: \( \frac{56 \div 8}{96 \div 8} = \frac{7}{12} \). Значит, угол \( AOB \) составляет \( \frac{7}{12} \) часть угла \( AOC \).

3) Аналогично найдем, какую часть от угла \( AOC \) составляет угол \( BOC \). Делим величину угла \( BOC \) на величину угла \( AOC \): \( 40 : 96 \). Запишем в виде дроби: \( \frac{40}{96} \). Найдем общий делитель числителя и знаменателя, это 8. Упростим дробь: \( \frac{40 \div 8}{96 \div 8} = \frac{5}{12} \). Следовательно, угол \( BOC \) составляет \( \frac{5}{12} \) часть угла \( AOC \). Таким образом, мы получили точные пропорции частей угла \( AOC \), которые занимают углы \( AOB \) и \( BOC \).