
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 727 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
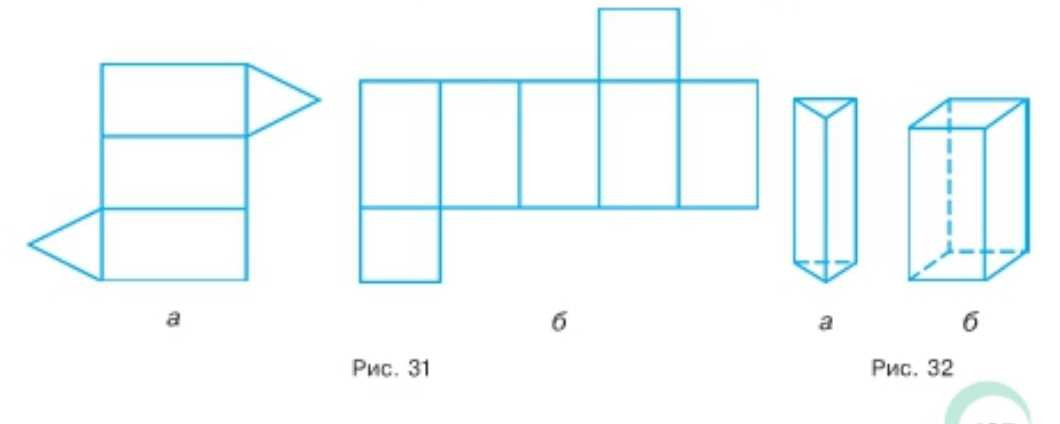
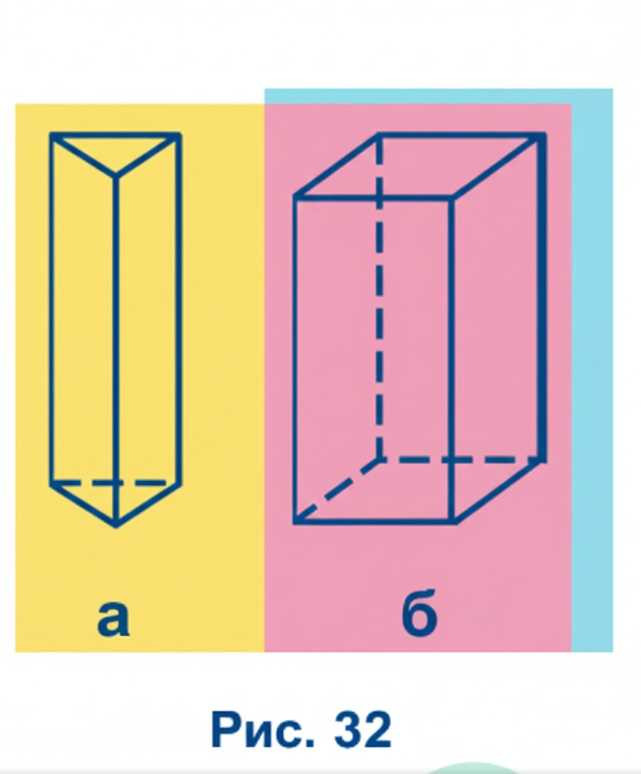
Вырежьте из плотной бумаги фигуры, изображённые на рисунке 31, и склейте фигуры, изображённые на рисунке 32. Эти фигуры называют призмами. У прямой призмы боковые грани — прямоугольники, а верхнее и нижнее основания — равные многоугольники. На рисунке 32, а изображена треугольная призма, а на рисунке 32, б — четырёхугольная. Каждый прямоугольный параллелепипед — это четырёхугольная призма.
Вырежьте фигуру, изображённую на рисунке 31, а, которая представляет собой развертку треугольной призмы. При склеивании боковые грани будут прямоугольниками, а верхнее и нижнее основания — равные треугольники, что соответствует определению треугольной призмы, показанной на рисунке 32, а.
Вырежьте фигуру, изображённую на рисунке 31, б, которая представляет собой развертку четырёхугольной призмы. При склеивании боковые грани станут прямоугольниками, а верхнее и нижнее основания — равными четырёхугольниками. Такая фигура соответствует четырёхугольной призме, изображённой на рисунке 32, б.
Таким образом, фигуры, вырезанные с рисунка 31, а и б, при склеивании образуют призмы: треугольную и четырёхугольную соответственно.
Вырезая фигуру, изображённую на рисунке 31, а, мы получаем развертку треугольной призмы. Эта фигура состоит из двух треугольников и трёх прямоугольников. При склеивании боковые стороны прямоугольников соединяются, образуя боковые грани призмы. Верхнее и нижнее основания — это равные треугольники, которые остаются параллельными и одинаковыми по форме и размеру. Именно такое сочетание граней и оснований соответствует определению треугольной призмы, показанной на рисунке 32, а. Важно понимать, что боковые грани призмы всегда являются прямоугольниками, а основания — равными многоугольниками, в данном случае треугольниками.
На рисунке 31, б изображена развертка четырёхугольной призмы. Она состоит из двух четырёхугольников и четырёх прямоугольников. При склеивании боковые прямоугольники соединяются, образуя боковые грани призмы, а верхнее и нижнее основания — это равные четырёхугольники. Такая фигура соответствует четырёхугольной призме, изображённой на рисунке 32, б. Каждый прямоугольный параллелепипед — это частный случай четырёхугольной призмы, где основания — прямоугольники, а боковые грани — также прямоугольники. Это подчёркивает связь между разверткой и объёмной фигурой.
Таким образом, вырезанные фигуры с рисунков 31, а и б, при правильном склеивании образуют призмы. Треугольная призма получается из развертки с треугольными основаниями и прямоугольными боковыми гранями, а четырёхугольная призма — из развертки с четырёхугольными основаниями и прямоугольными боковыми гранями. Это наглядно демонстрирует, что призма — это объёмная фигура, у которой боковые грани — прямоугольники, а верхнее и нижнее основания — равные многоугольники.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!