
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 679 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
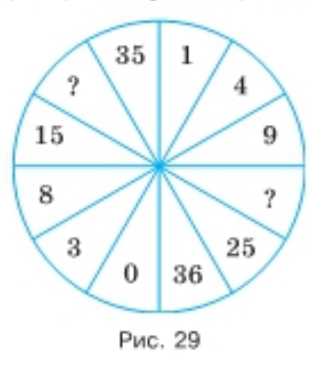
Найдите правило размещения чисел в полукругах и вставьте недостающие числа (рис. 29).
В правой половине круга стоят квадраты натуральных чисел по часовой стрелке: \(1=1^2\), \(4=2^2\), \(9=3^2\), \(16=4^2\), \(25=5^2\), \(36=6^2\). Следовательно, в правом нижнем секторе уже есть \(16\), а в правом верхнем должен быть следующий квадрат \(49=7^2\), но сектора ограничены до показанных значений, поэтому неизвестные именно напротив левых чисел.
В левой половине сумма растёт, прибавляя подряд нечетные числа: \(0\to 3\) (\(+3\)), \(3\to 8\) (\(+5\)), \(8\to 15\) (\(+7\)), \(15\to 24\) (\(+9\)), \(24\to 35\) (\(+11\)). Следующие прибавления: \(+13\) и \(+15\).
Отсюда недостающие значения: над \(24\) справа сверху должен стоять \(49\), а под \(16\) справа снизу уже \(25\) есть. Для левой ветки после \(35\) будет \(35+13=48\).
Ответ: \(49\) и \(48\).
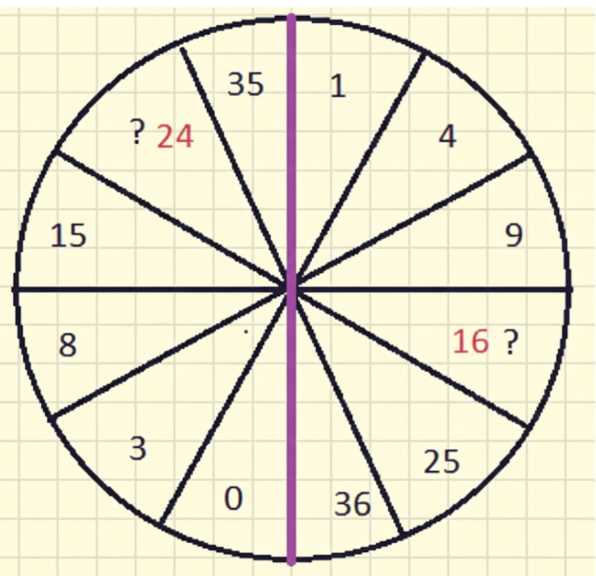
В правой части круга числа организованы как квадраты натуральных последовательных чисел по часовой стрелке. Это видно по цепочке: \(1=1^{2}\), \(4=2^{2}\), \(9=3^{2}\), \(16=4^{2}\), \(25=5^{2}\), \(36=6^{2}\). Следовательно, закономерность проста: каждый следующий сектор справа содержит \(n^{2}\) при увеличении \(n\) на единицу. Раз в правом верхнем секторе стоит знак вопроса рядом с уже имеющимися квадратами, то после \(36=6^{2}\) следующий квадрат равен \(49=7^{2}\). Именно он заполняет пустое место на правой стороне там, где требуется продолжение ряда квадратов.
Левая часть формирует возрастающую последовательность сумм, получаемых добавлением подряд идущих нечетных чисел. Проверим шаги на имеющихся значениях: \(0\to 3\) есть прибавление \(+3\), далее \(3\to 8\) есть прибавление \(+5\), затем \(8\to 15\) даёт \(+7\), далее \(15\to 24\) это \(+9\), и \(24\to 35\) это \(+11\). Видно правило: каждый следующий прирост увеличивается на \(2\), то есть используется последовательность нечетных чисел \(3,5,7,9,11,\dots\). Следующий шаг по этой логике должен добавить \(+13\), затем последующий \(+15\), и так далее, если продолжать.
Так как знак вопроса на левой стороне стоит после числа \(35\), применяем следующий шаг последовательности нечетных прибавок: \(35+13=48\). Итого недостающие значения определяются одновременно из двух независимых закономерностей: справа продолжение квадратов даёт \(49=7^{2}\), слева продолжение сумм с прибавлением нечетных чисел даёт \(48\). Ответ: \(49\) и \(48\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!