ГДЗ по Математике 6 Класс Часть 1 Номер 677 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

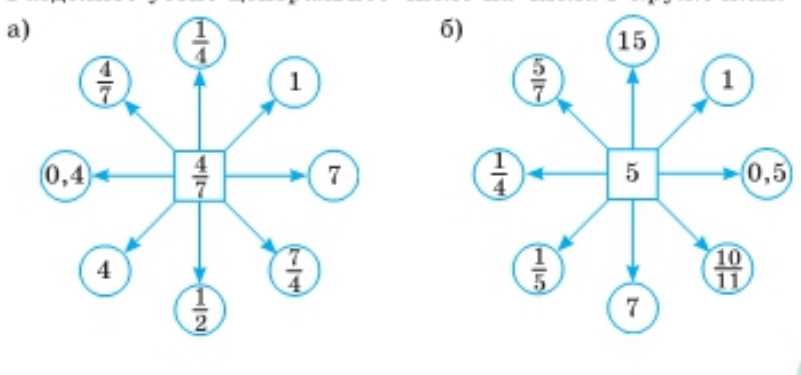
Разделите устно центральное число на числа в кружочках.

Вот краткое решение по каждому пункту, соответствующее изображению, с пояснением шага деления дробей и чисел.

a) Деление дробей выполняем умножением на обратную дробь, затем сокращаем.

\( \frac{4}{7} : \frac{1}{4} = \frac{4}{7} \cdot \frac{4}{1} = \frac{16}{7} = 2\frac{2}{7} \)

\( \frac{4}{7} : 1 = \frac{4}{7} \)

\( \frac{4}{7} : 7 = \frac{4}{7} \cdot \frac{1}{7} = \frac{4}{49} \)

\( \frac{4}{7} : \frac{7}{4} = \frac{4}{7} \cdot \frac{4}{7} = \frac{16}{49} \)

\( \frac{4}{7} : \frac{1}{2} = \frac{4}{7} \cdot \frac{2}{1} = \frac{8}{7} = 1\frac{1}{7} \)

\( \frac{4}{7} : 4 = \frac{4}{7} \cdot \frac{1}{4} = \frac{1}{7} \)

\( \frac{4}{7} : 0{,}4 = \frac{4}{7} : \frac{2}{5} = \frac{4}{7} \cdot \frac{5}{2} = \frac{20}{14} = \frac{10}{7} = 1\frac{3}{7} \)

\( \frac{4}{7} : \frac{4}{7} = 1 \)

б) Деление на дробь заменяем умножением на обратную; деление на число трактуем как умножение на его обратное.

\( 5 : 15 = \frac{5}{15} = \frac{1}{3} \)

\( 5 : 1 = 5 \)

\( 5 : 0{,}5 = 5 \cdot \frac{1}{0{,}5} = 5 \cdot 2 = 10 \)

\( 5 : \frac{10}{11} = 5 \cdot \frac{11}{10} = \frac{55}{10} = \frac{11}{2} = 5{,}5 \)

\( 5 : 7 = \frac{5}{7} \)

\( 5 : \frac{1}{5} = 5 \cdot 5 = 25 \)

\( 5 : \frac{1}{4} = 5 \cdot 4 = 20 \)

\( 5 : \frac{5}{7} = 5 \cdot \frac{7}{5} = 7 \)

a) При делении дробей используем правило: деление заменяем умножением на обратную дробь, после чего выполняем сокращение и, при необходимости, переводим неправильную дробь в смешанное число. Для деления на целое число \(n\) умножаем на дробь \(\frac{1}{n}\); для десятичного числа сначала переводим его в обыкновенную дробь.

\( \frac{4}{7} : \frac{1}{4} = \frac{4}{7} \cdot \frac{4}{1} = \frac{16}{7} = 2\frac{2}{7} \). Здесь обратная к \(\frac{1}{4}\) равна \(\frac{4}{1}\); умножение числителей и знаменателей даёт неправильную дробь, которую превращаем в смешанную: \(16 = 2 \cdot 7 + 2\).

\( \frac{4}{7} : 1 = \frac{4}{7} \). Деление на единицу не изменяет значение дроби.

\( \frac{4}{7} : 7 = \frac{4}{7} \cdot \frac{1}{7} = \frac{4}{49} \). Деление на целое \(7\) заменили умножением на \(\frac{1}{7}\); знаменатель увеличился в \(7\) раз.

\( \frac{4}{7} : \frac{7}{4} = \frac{4}{7} \cdot \frac{4}{7} = \frac{16}{49} \). Обратная к \(\frac{7}{4}\) есть \(\frac{4}{7}\); произведение даёт квадрат числителя и знаменателя: \(4^{2} = 16\), \(7^{2} = 49\).

\( \frac{4}{7} : \frac{1}{2} = \frac{4}{7} \cdot \frac{2}{1} = \frac{8}{7} = 1\frac{1}{7} \). Получили неправильную дробь; \(8 = 1 \cdot 7 + 1\), потому переводим в смешанную.

\( \frac{4}{7} : 4 = \frac{4}{7} \cdot \frac{1}{4} = \frac{4}{28} = \frac{1}{7} \). Сократили на \(4\), получив простой результат.

\( \frac{4}{7} : 0{,}4 = \frac{4}{7} : \frac{2}{5} = \frac{4}{7} \cdot \frac{5}{2} = \frac{20}{14} = \frac{10}{7} = 1\frac{3}{7} \). Десятичное \(0{,}4\) преобразовали в \(\frac{2}{5}\); после умножения сократили на \(2\); затем перевели неправильную дробь: \(10 = 1 \cdot 7 + 3\).

\( \frac{4}{7} : \frac{4}{7} = 1 \). Любая ненулевая дробь при делении на саму себя равна единице.

б) Для целых и десятичных чисел действуем аналогично: деление заменяем умножением на обратное, для десятичного числа используем эквивалентную дробь; при необходимости сокращаем и переводим в смешанное число или десятичную форму.

\( 5 : 15 = \frac{5}{15} = \frac{1}{3} \). Деление целого на целое трактуем как дробь; сокращаем на \(5\).

\( 5 : 1 = 5 \). Деление на единицу не изменяет число.

\( 5 : 0{,}5 = 5 \cdot \frac{1}{0{,}5} = 5 \cdot 2 = 10 \). Использовали факт \(0{,}5 = \frac{1}{2}\), значит обратное равно \(2\).

\( 5 : \frac{10}{11} = 5 \cdot \frac{11}{10} = \frac{55}{10} = \frac{11}{2} = 5{,}5 \). Умножили на обратную дробь, сократили на \(5\), затем представили результат в десятичной форме.

\( 5 : 7 = \frac{5}{7} \). Представление деления двух целых как дроби.

\( 5 : \frac{1}{5} = 5 \cdot 5 = 25 \). Деление на дробь меньше единицы эквивалентно умножению на её обратную, что увеличивает число.

\( 5 : \frac{1}{4} = 5 \cdot 4 = 20 \). Аналогично предыдущему случаю: обратная к \(\frac{1}{4}\) равна \(4\).

\( 5 : \frac{5}{7} = 5 \cdot \frac{7}{5} = 7 \). Сокращение \(5\) в числителе и знаменателе даёт целый результат.