ГДЗ по Математике 6 Класс Часть 1 Номер 616 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

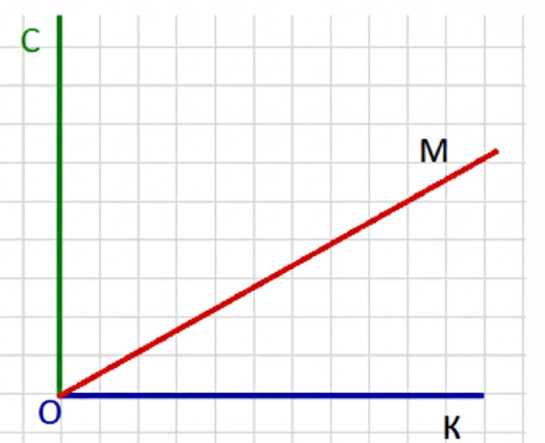
Луч ОМ разделил угол СОК, равный \(90^\circ\), на два угла СОМ и МОК. Угол СОМ больше угла МОК в \(2\frac{3}{5}\) раза. Чему равны углы СОМ и МОК? Постройте эти углы с помощью транспортира.

Пусть \(\angle MOK = x^\circ\), а \(\angle COM = \frac{13}{5}x^\circ\). Вместе они дают \(90^\circ\), значит \(x + \frac{13}{5}x = 90\).

Складываем: \(\frac{18}{5}x = 90\), откуда \(x = 90 \cdot \frac{5}{18} = 25^\circ\). Тогда \(\angle MOK = 25^\circ\).

Находим второй угол: \(\angle COM = 90^\circ — 25^\circ = 65^\circ\).

Пусть \(\angle MOK = x^\circ\). По условию второй угол выражается через первый как \(\angle COM = \frac{13}{5}x^\circ\). Эти два угла составляют прямой угол, то есть их сумма равна \(90^\circ\). Составим уравнение на основании суммы смежных углов: \(x^\circ + \frac{13}{5}x^\circ = 90^\circ\). Здесь обе части равенства имеют размерность градусов, поэтому далее можно оперировать только коэффициентами при \(x\).

Сложим коэффициенты при \(x\): \(1 + \frac{13}{5} = \frac{5}{5} + \frac{13}{5} = \frac{18}{5}\). Тогда получаем линейное уравнение \(\frac{18}{5}x = 90\). Чтобы найти \(x\), умножаем обе части уравнения на \(\frac{5}{18}\), что является обратным числом к \(\frac{18}{5}\): \(x = 90 \cdot \frac{5}{18}\). Выполним упрощение: \(90 \div 18 = 5\), следовательно \(x = 5 \cdot 5 = 25\). Значит \(\angle MOK = 25^\circ\).

Теперь вычислим второй угол. Так как сумма углов равна \(90^\circ\), то \(\angle COM = 90^\circ — 25^\circ = 65^\circ\). Проверим согласованность с исходной пропорцией: \(\frac{13}{5} \cdot 25^\circ = 13 \cdot 5^\circ = 65^\circ\), что совпадает с найденным значением. Итог: \(\angle MOK = 25^\circ\) и \(\angle COM = 65^\circ\).