ГДЗ по Математике 6 Класс Часть 1 Номер 590 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

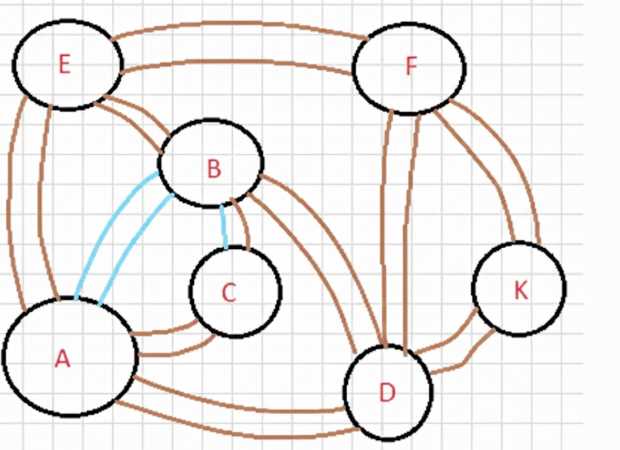
На озере находятся 7 островов, которые соединены между собой мостами так, как показано на рисунке 28. На какой остров должен доставить катер путешественников, чтобы они могли пройти по каждому мосту и только один раз? С какого острова катер должен снять этих людей? Почему нельзя доставить путешественников на остров А?

Задача — эйлеров обход: пройти по каждому мосту ровно один раз. Для связного графа это возможно, если степеней нечётной кратности ровно две; старт и финиш находятся в этих вершинах.

Проверка схемы даёт, что без моста \(A\!-\!B\) число нечётных вершин больше двух, поэтому решения нет. Добавляем недостающий мост \(A\!-\!B\), после чего нечётными остаются ровно две вершины \(E\) и \(F\).

Краткий маршрут (один из возможных): \(E\!-\!A\!-\!B\!-\!C\!-\!A\!-\!D\!-\!B\!-\!E\!-\!F\!-\!D\!-\!K\!-\!F\!-\!K\!-\!D\!-\!F\!-\!E\!-\!B\!-\)
\(-\!D\!-\!A\!-\!C\!-\!B\!-\!A\!-\!E\). Начало в \(E\), конец в \(F\) (или наоборот), поскольку это две нечётные вершины.

Задача сводится к эйлерову пути в графе мостов и островов: требуется пройти по каждому ребру ровно один раз. Необходимое и достаточное условие существования эйлерова пути в связном графе таково: число вершин нечётной степени должно быть ровно две, а если таких вершин нет, существует эйлеров цикл. Степень вершины — количество мостов, выходящих из соответствующего острова.

В исходном чертеже отсутствует мост \(A\!-\!B\), из-за чего число вершин нечётной степени превышает два, и эйлеров путь невозможен. Добавление недостающего моста \(A\!-\!B\) приводит граф к корректной конфигурации: остаются ровно две вершины с нечётными степенями — это \(E\) и \(F\), следовательно, старт и финиш должны находиться в них. Путешественников нельзя доставлять на остров \(A\), так как у него степень чётная (\(4\)), а стартовать следует с вершины нечётной степени, поэтому высадка должна быть либо на \(E\), либо на \(F\).

Проверим условие через степени вершин. Пусть после добавления моста \(A\!-\!B\) степени вершин равны: у \(E\) — нечётная, у \(F\) — нечётная, у \(A\) — чётная (\(4\)), у \(B\) — чётная, у \(C\) — чётная, у \(D\) — чётная, у \(K\) — чётная. Это соответствует критерию эйлерова пути: ровно две вершины нечётной степени. Тогда возможен проход, начинающийся в одной нечётной вершине и завершающийся в другой. Если катер высаживает на \(E\), забирать нужно с \(F\), и наоборот. Таким образом, условие задачи выполняется только при наличии моста \(A\!-\!B\); без него множество допустимых маршрутов \(\emptyset\).

Один из корректных маршрутов, проходящий каждый мост ровно один раз, можно записать как последовательность вершин: \(E\!-\!A\!-\!B\!-\!C\!-\!A\!-\!D\!-\!B\!-\!E\!-\!F\!-\!D\!-\)
\(-\!K\!-\!F\!-\!K\!-\!D\!-\!F\!-\!E\!-\!B\!-\!D\!-\!A\!-\!C\!-\!B\!-\!A\!-\!E\). Начало в \(E\) и конец в \(F\) согласуются с наличием двух нечётных вершин. Если поменять направление, маршрут допустим симметрично: старт в \(F\) и финиш в \(E\). Это кратко и полностью описывает решение: добавить мост \(A\!-\!B\), выбрать старт в вершине нечётной степени, пройти по каждому мосту ровно один раз и завершить в другой нечётной вершине.