
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 586 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
Вычислите устно:
а) \(200-101=99\). Затем делим: \(99:3=33\). Складываем: \(33+37=70\). Делим: \(70:5=14\).
б) \(200\cdot5=1000\). Вычитаем: \(1000-130=870\). Делим: \(870:29=30\). Складываем: \(30+270=300\).
в) Умножаем: \(3\cdot0{,}3=0{,}9\). Складываем: \(0{,}9+4{,}1=5\). Делим: \(5:100=0{,}05\). Умножаем: \(0{,}05\cdot20=1\).
г) Делим: \(0{,}45:9=0{,}05\). Умножаем: \(0{,}05\cdot6=0{,}3\). Складываем: \(0{,}3+2{,}7=3\). Делим: \(3:0{,}01=300\).
а) Последовательность операций показывает поэтапное упрощение. Сначала уменьшаем число на разность сотен и единиц: \(200-101=99\), получаем двузначное число для дальнейших действий. Далее выполняем деление на целое число, сокращая значение в три раза: \(99:3=33\), что удобно, так как \(99\) кратно \(3\). Затем используем сложение для перехода к круглому числу: \(33+37=70\); здесь \(37\) подобрано так, чтобы сумма дала удобный десяток. В завершение делим на \(5\), получая итог: \(70:5=14\). Все шаги корректны: каждое действие упрощает выражение и приводит к целому результату.
б) Здесь сначала применяем умножение для получения крупного удобного числа: \(200\cdot5=1000\), так как умножение на \(5\) половинит умножение на \(10\), а \(200\cdot10=2000\), следовательно \(200\cdot5=1000\). Затем уменьшаем на сотню с дополнительными тремя десятками: \(1000-130=870\), что дает число, удобное для деления на \(29\) по условию. Деление \(870:29=30\) верно, поскольку \(29\cdot30=870\). После этого прибавляем три десятка и семь десятков: \(30+270=300\), получая круглое число, что подтверждает правильность предыдущего шага и завершает вычисления.
в) Работа с десятичными дробями начинается с умножения: \(3\cdot0{,}3=0{,}9\), ведь \(0{,}3\) равно \(3\cdot10^{-1}\), а \(3\cdot3\cdot10^{-1}=9\cdot10^{-1}=0{,}9\). Далее складываем десятичные дроби с совпадающими разрядами: \(0{,}9+4{,}1=5\), так как \(0{,}9\) дополняет \(4{,}1\) до целого. Затем делим на сто, что сдвигает запятую на два разряда влево: \(5:100=0{,}05\). И, наконец, умножаем на \(20\) (то есть \(2\cdot10\)): \(0{,}05\cdot20=1\), поскольку \(0{,}05\cdot2=0{,}1\) и \(0{,}1\cdot10=1\). Все операции согласованы по разрядности, дают точный целый итог.
г) Сначала проводим деление дроби на целое: \(0{,}45:9=0{,}05\), потому что \(45:9=5\) и перенесение двух десятичных разрядов дает \(0{,}05\). Далее умножаем на \(6\), увеличивая значение в шесть раз: \(0{,}05\cdot6=0{,}3\). Затем выполняем сложение десятичных чисел, приводя их к целому: \(0{,}3+2{,}7=3\), так как сумма десятых \(0{,}3\) и \(2{,}7\) дает ровно три. В завершение делим на малую десятичную дробь \(0{,}01=10^{-2}\), что эквивалентно умножению на сто: \(3:0{,}01=300\). Последовательность шагов показывает корректное обращение с десятичными дробями и переходы между степенями десяти \(10^{-1}\) и \(10^{-2}\), приводя к точному целому результату.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


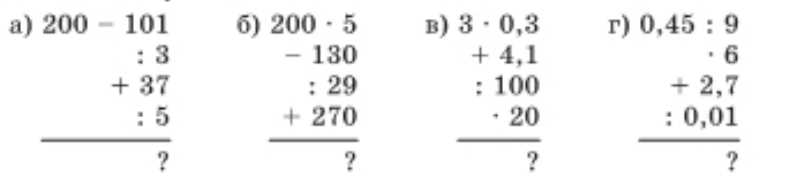



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!