ГДЗ по Математике 6 Класс Часть 1 Номер 561 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

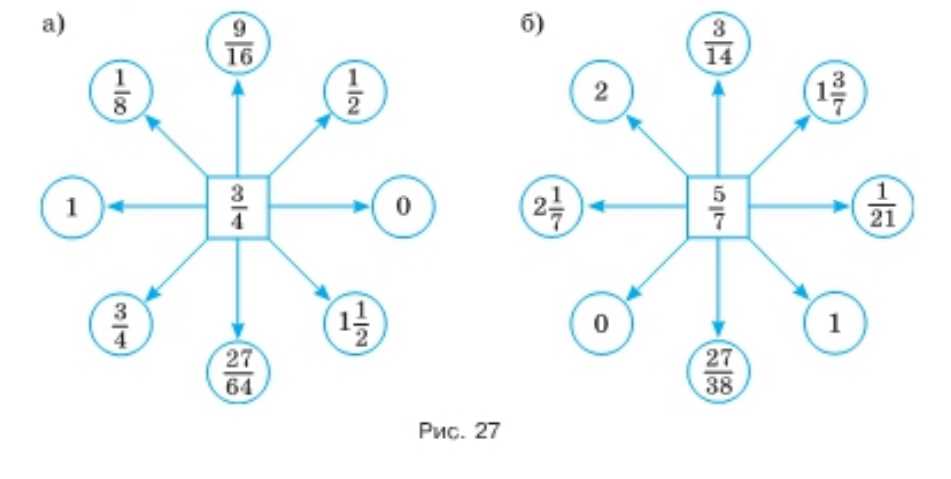
Подумайте, как из числа, записанного в центре (рис. 27), можно получить числа, записанные в кружках.

a) \( \frac{3}{4}\cdot\frac{3}{4}=\frac{9}{16} \). Перемножаем числители и знаменатели, сокращений нет.

\( \frac{3}{4}:\frac{4}{6}=\frac{3}{4}\cdot\frac{6}{4}=\frac{18}{16}=\frac{9}{8}=1\frac{1}{8} \). Деление заменяем умножением на обратную дробь и сокращаем на \(2\).

\( \frac{3}{4}\cdot0=0 \). Произведение любого числа на ноль равно нулю.

\( \frac{3}{4}:\frac{4}{2}=\frac{3}{4}\cdot\frac{2}{4}=\frac{6}{16}=\frac{3}{8} \). Обращаем делитель и сокращаем на \(2\).

\( \frac{3}{4}\cdot\frac{9}{16}=\frac{27}{64} \). Умножаем дроби, общий делитель отсутствует.

\( \frac{3}{4}:1=\frac{3}{4} \). Деление на единицу не меняет значение.

\( \frac{3}{4}:\frac{4}{3}=\frac{3}{4}\cdot\frac{3}{4}=\frac{9}{16} \). Делим на дробь, умножая на обратную.

\( \frac{3}{4}:\frac{5}{6}=\frac{3}{4}\cdot\frac{6}{5}=\frac{18}{20}=\frac{9}{10} \). Сокращаем на \(2\).

\( \frac{3}{4}:\frac{6}{8}=\frac{3}{4}\cdot\frac{8}{6}=\frac{24}{24}=1 \). Равные числитель и знаменатель дают единицу.

б) \( \frac{5}{7}-\frac{1}{2}=\frac{10}{14}-\frac{7}{14}=\frac{3}{14} \). Приводим к общему знаменателю \(14\) и вычитаем.

\( \frac{5}{7}\cdot2=\frac{10}{7}=1\frac{3}{7} \). Умножаем числитель и выделяем целую часть.

\( \frac{5}{7}\cdot\frac{1}{15}=\frac{5}{105}=\frac{1}{21} \). Сокращаем на \(5\).

\( \frac{5}{7}:\frac{5}{7}=1 \). Дробь, делённая на себя, равна единице.

\( \frac{5}{7}:1\frac{1}{189}=\frac{5}{7}:\frac{190}{189}=\frac{5}{7}\cdot\frac{189}{190}=\frac{945}{1330}=\frac{27}{38} \). Переводим смешанное в неправильную, умножаем на обратную и сокращаем на \(35\).

\( \frac{5}{7}\cdot0=0 \). Умножение на ноль даёт ноль.

\( \frac{5}{7}+1\frac{3}{7}=\frac{5}{7}+\frac{10}{7}=\frac{15}{7}=2\frac{1}{7} \). Переводим смешанное число и выделяем целую часть.

\( \frac{5}{7}+1\frac{2}{7}=\frac{5}{7}+\frac{9}{7}=\frac{14}{7}=2 \). Складываем числители при одинаковом знаменателе и делим.

a) \( \frac{3}{4}\cdot\frac{3}{4}=\frac{3\cdot3}{4\cdot4}=\frac{9}{16} \). Перемножаем числители и знаменатели по правилу умножения дробей; дробь уже несократима, так как \(9\) и \(16\) не имеют общих делителей кроме \(1\).

\( \frac{3}{4}:\frac{4}{6}=\frac{3}{4}\cdot\frac{6}{4}=\frac{18}{16}=\frac{9}{8}=1\frac{1}{8} \). Деление заменяем умножением на обратную дробь; сокращаем \(18\) и \(16\) на \(2\), получаем неправильную дробь \(\frac{9}{8}\); выделяем целую часть: \(9=8+1\), значит \(1\frac{1}{8}\).

\( \frac{3}{4}\cdot0=0 \). При умножении любого числа на ноль результат равен нулю, дополнительных преобразований не требуется.

\( \frac{3}{4}:\frac{4}{2}=\frac{3}{4}\cdot\frac{2}{4}=\frac{6}{16}=\frac{3}{8} \). Сначала обращаем делитель, затем сокращаем числитель и знаменатель на \(2\), получая правильную дробь со знаменателем \(8\).

\( \frac{3}{4}\cdot\frac{9}{16}=\frac{3\cdot9}{4\cdot16}=\frac{27}{64} \). Здесь сокращения нет: общий делитель \(27\) и \(64\) равен \(1\); оставляем результат в виде несократимой дроби.

\( \frac{3}{4}:1=\frac{3}{4} \). Деление на единицу не изменяет значение числа; дробная запись сохраняется без изменения числителя и знаменателя.

\( \frac{3}{4}:\frac{4}{3}=\frac{3}{4}\cdot\frac{3}{4}=\frac{9}{16} \). Переворачиваем делитель \(\frac{4}{3}\rightarrow\frac{3}{4}\) и перемножаем; результат совпадает с первым пунктом по структуре.

\( \frac{3}{4}:\frac{5}{6}=\frac{3}{4}\cdot\frac{6}{5}=\frac{18}{20}=\frac{9}{10} \). Сокращаем числитель и знаменатель на \(2\); получаем правильную несократимую дробь со знаменателем \(10\).

\( \frac{3}{4}:\frac{6}{8}=\frac{3}{4}\cdot\frac{8}{6}=\frac{24}{24}=1 \). Перед умножением можно сократить \( \frac{8}{6} \) до \( \frac{4}{3} \), но даже без этого произведение даёт равные числитель и знаменатель, что равно единице.

б) \( \frac{5}{7}-\frac{1}{2}=\frac{10}{14}-\frac{7}{14}=\frac{3}{14} \). Приводим к общему знаменателю \(14\): домножаем первую дробь на \(2\), вторую на \(7\); вычитаем числители \(10-7=3\); дробь \(\frac{3}{14}\) несократима.

\( \frac{5}{7}\cdot2=\frac{5\cdot2}{7}=\frac{10}{7}=1\frac{3}{7} \). Умножение на целое сводится к умножению числителя; выделяем целую часть: \(10=7+3\), получаем \(1\frac{3}{7}\).

\( \frac{5}{7}\cdot\frac{1}{15}=\frac{5\cdot1}{7\cdot15}=\frac{5}{105}=\frac{1}{21} \). Сокращаем числитель и знаменатель на общий делитель \(5\); итоговая дробь простая и правильная.

\( \frac{5}{7}:\frac{5}{7}=\frac{5}{7}\cdot\frac{7}{5}=\frac{35}{35}=1 \). Любая ненулевая дробь при делении сама на себя даёт единицу; после обращения множители взаимно уничтожаются.

\( \frac{5}{7}:1\frac{1}{189}=\frac{5}{7}:\frac{190}{189}=\frac{5}{7}\cdot\frac{189}{190}=\frac{5\cdot189}{7\cdot190}=\frac{945}{1330}=\frac{27}{38} \). Смешанную дробь переводим в неправильную: \(1\frac{1}{189}=\frac{190}{189}\); обращаем делитель; сокращаем: \(945\) и \(1330\) делятся на \(35\), получаем несократимую \(\frac{27}{38}\).

\( \frac{5}{7}\cdot0=0 \). По свойству нуля произведение равно нулю, дополнительных преобразований не проводится.

\( \frac{5}{7}+1\frac{3}{7}=\frac{5}{7}+\frac{10}{7}=\frac{15}{7}=2\frac{1}{7} \). Сначала переводим смешанное число \(1\frac{3}{7}=\frac{10}{7}\); знаменатели одинаковые, складываем числители \(5+10=15\); выделяем \(2\) целых и \(\frac{1}{7}\).

\( \frac{5}{7}+1\frac{2}{7}=\frac{5}{7}+\frac{9}{7}=\frac{14}{7}=2 \). Переводим смешанное \(1\frac{2}{7}=\frac{9}{7}\); сумма числителей \(5+9=14\); делим на знаменатель \(7\), получаем целое число \(2\).