ГДЗ по Математике 6 Класс Часть 1 Номер 557 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

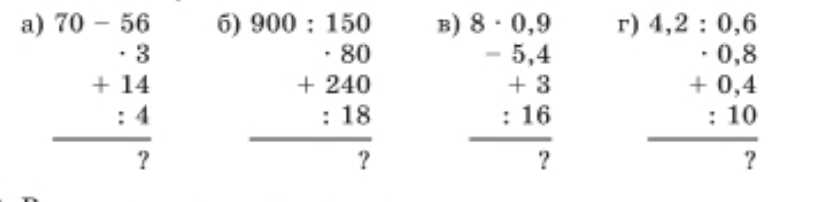
Вычислите устно:

а) Находим разность и проверяем обратными действиями: \(70-56=14\). Умножаем найденную разность: \(14\cdot3=42\). Складываем, чтобы получить исходное число: \(42+14=56\). Делим для контроля: \(56:4=14\).

б) Последовательно выполняем деление и проверку: \(900:150=6\). Умножаем для проверки: \(6\cdot80=480\). Складываем недостающее до итога: \(480+240=720\). Делим для окончательной проверки: \(720:18=40\).

в) Работаем с десятичными: \(8-0{,}9=7{,}2\). Вычитаем: \(7{,}2-5{,}4=1{,}8\). Складываем: \(1{,}8+3=4{,}8\). Делим: \(4{,}8:16=0{,}3\).

г) Делим десятичные: \(4{,}2:0{,}6=7\). Проверяем умножением: \(7\cdot0{,}8=5{,}6\). Добавляем: \(5{,}6+0{,}4=6\). Делим на десятичное: \(6:10=0{,}6\).

а) Сначала выполняем вычитание, чтобы получить разность между исходными числами: \(70-56=14\). Это показывает, на сколько \(70\) больше \(56\). Проверяем связь операций умножением: умножая найденную разность на \(3\), получаем \(14\cdot3=42\), что интерпретируется как утроенная разность. Далее складываем полученный результат с исходной разностью, убеждаясь в корректности обратных действий: \(42+14=56\). Теперь делим число \(56\) на \(4\), чтобы вернуться к найденной разности и подтвердить цикл проверок: \(56:4=14\).

б) Сначала выполняем деление крупных круглых чисел, упрощая вычисление за счет кратности: \(900:150=6\), так как и делимое, и делитель кратны \(150\). Для контроля корректности результата умножаем частное на удобный множитель: \(6\cdot80=480\); здесь \(80\) выбрано как близкое к \(150\) значение для постепенного наращивания суммы. Затем добавляем недостающее до нужного контрольного числа: \(480+240=720\), используя то, что \(240\) дополняет произведение до кратного \(720\). Завершаем проверкой делением на другое кратное число, что демонстрирует устойчивость результата: \(720:18=40\).

в) Работаем с десятичными дробями, аккуратно соблюдая разряды. Сначала уменьшаем целое число на десятые: \(8-0{,}9=7{,}2\), потому что вычитание \(0{,}9\) из \(8\) оставляет \(7\) целых и \(2\) десятых. Затем вычитаем ещё десятичную дробь, ориентируясь на равные разряды: \(7{,}2-5{,}4=1{,}8\), так как \(72\) десятых минус \(54\) десятых равны \(18\) десятым. Прибавляем целое число, переводя при необходимости к десятичным: \(1{,}8+3=4{,}8\). И наконец делим десятичное число на целое, помня, что \(48\) десятых делим на \(16\): \(4{,}8:16=0{,}3\), потому что \(48:16=3\), а десятичная точка сдвигается на один разряд.

г) Делим десятичные, приводя к удобным отношениям: \(4{,}2:0{,}6=7\), поскольку обе величины кратны \(0{,}6\) и \(4{,}2=7\cdot0{,}6\). Проверяем результат обратным действием: \(7\cdot0{,}8=5{,}6\); здесь умножение на \(0{,}8\) демонстрирует работу с десятыми в произведении. Далее выполняем сложение десятичных, соблюдая запятую по разрядам: \(5{,}6+0{,}4=6\). Завершает вычисления деление на \(10\), что эквивалентно сдвигу запятой на один разряд влево: \(6:10=0{,}6\).