ГДЗ по Математике 6 Класс Часть 1 Номер 540 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

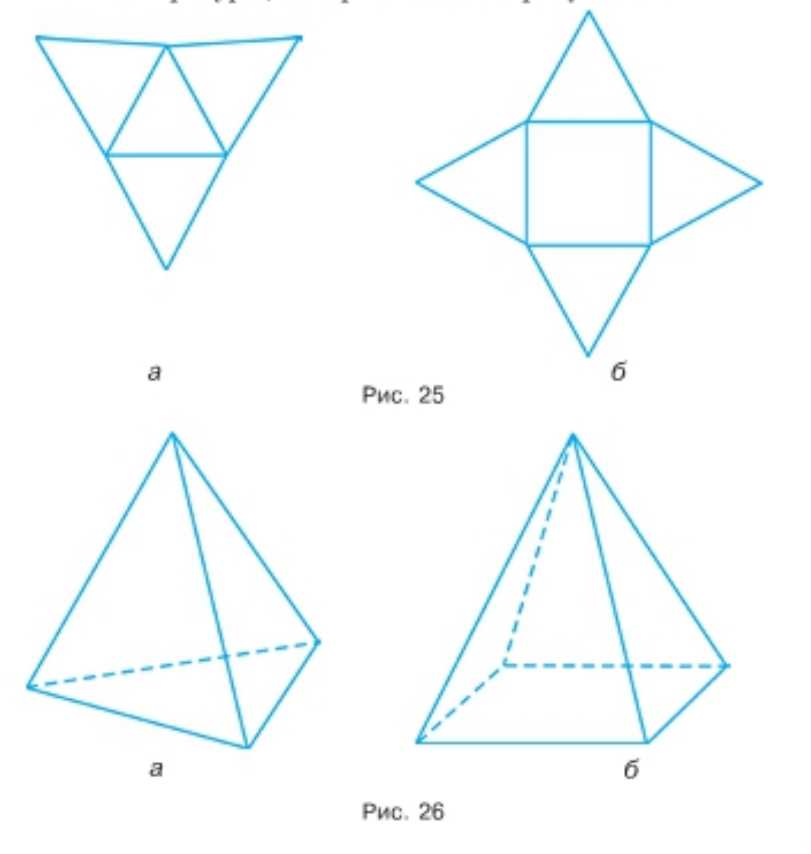
Вырежьте из плотной бумаги фигуры, показанные на рисунке 25, и склейте фигуры, изображённые на рисунке 26.

Под буквой а) вырежьте треугольный развёртку с четырьмя равными треугольниками и склейте по рёбрам: получится треугольная пирамида с основанием-треугольником и тремя боковыми гранями-треугольниками. Высота идёт от вершины к центру основания.

Под буквой б) вырежьте квадрат с четырьмя равными треугольниками по сторонам и склейте по рёбрам: получится четырёхугольная пирамида с основанием-квадратом и четырьмя боковыми гранями-треугольниками. Высота идёт от вершины к центру квадрата.

Для а) подготовьте развёртку из четырёх равных треугольников: центральный треугольник — основание, три боковых — грани. Аккуратно проведите линии сгиба по рёбрам, совместите стороны центрального треугольника с соответствующими сторонами боковых треугольников и склейте. В результате получится треугольная пирамида (тетраэдрическая форма с одним выделенным основанием): три боковые грани — равные треугольники, основание — треугольник. Высота пирамиды — перпендикуляр от вершины к плоскости основания. Если основание равностороннее со стороной \(a\), то площадь основания равна \(S_{b}=\frac{\sqrt{3}}{4}a^{2}\), а при высоте \(h\) объём равен \(V=\frac{1}{3}S_{b}h\).

Для б) подготовьте квадрат и четыре равных треугольника, расположенных по его сторонам: квадрат — основание, треугольники — боковые грани. Согните по границам квадрата, приподнимите треугольники, сведите их вершины в одну точку и склейте смежные рёбра. Получится четырёхугольная пирамида: основание — квадрат, боковых граней четыре, каждая — треугольник. Высота проходит от общей вершины к центру квадрата. Если квадрат имеет сторону \(a\), то площадь основания равна \(S_{b}=a^{2}\), а при высоте \(h\) объём равен \(V=\frac{1}{3}S_{b}h=\frac{1}{3}a^{2}h\).

Для прочности используйте плотную бумагу, делайте надрезы только по предназначенным линиям склейки и формируйте чёткие сгибы. Совмещение рёбер выполняйте попарно: в а) три пары рёбер вокруг треугольника основания, в б) четыре пары рёбер вокруг квадрата. Контролируйте перпендикулярность высоты к основанию: в а) вершина должна проецироваться в центр треугольника, в б) в центр квадрата. При необходимости пометьте рёбра одинаковыми метками, чтобы склейка шла последовательно; итоговые фигуры совпадают с изображениями: а) треугольная пирамида, б) четырёхугольная пирамида.