ГДЗ по Математике 6 Класс Часть 1 Номер 517 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

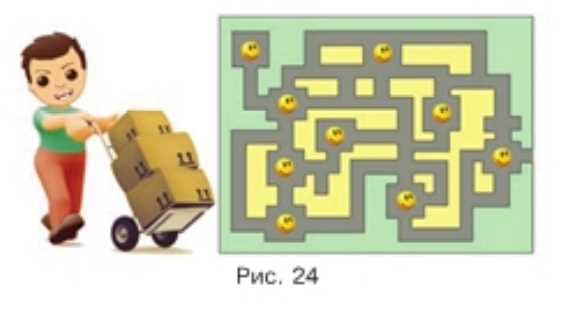
Нужно срочно доставить 9 пакетов в пункты, указанные на плане (рис. 24). Посыльный, посмотрев на план, быстро сообразил, как ему ехать. Он вручил пакеты, объехав пункты, ни разу не проезжая дважды одним и тем же путём. Какой маршрут выбрал посыльный?

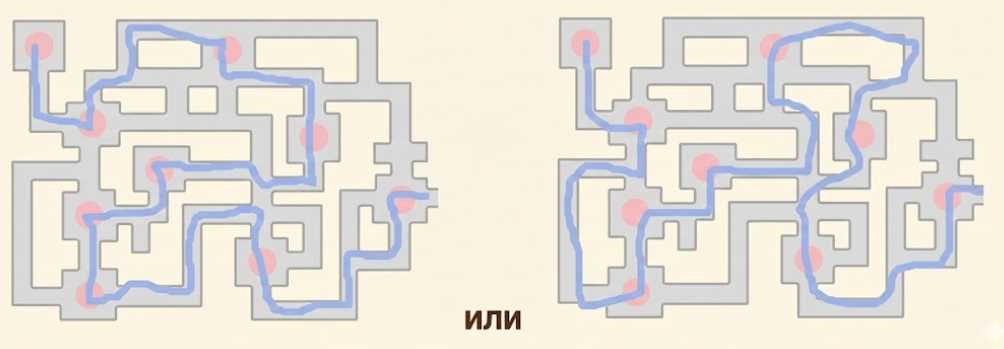
Посыльный выбрал маршрут, проходящий все точки один раз по типу эйлерова пути.

Краткое решение: дороги на плане образуют граф. Чтобы объехать все пункты, не повторяя путь, нужен эйлеров путь. На схеме ровно две вершины имеют нечётные степени, значит существует эйлеров путь, который начинается в одной из этих вершин и заканчивается в другой. Маршрут: вход слева снизу → последовательно обход нижнего коридора к правому краю → подъём по правым ответвлениям с посещением правых точек → переход через верхний коридор с посещением верхних точек → спуск через центральные ответвления к левым точкам → выход слева сверху.

Маршрут посыльного строится как эйлеров путь по дорожной сети плана. Рассматриваем коридоры как рёбра графа, а перекрёстки и тупики как вершины. Условие «ни разу не проезжая дважды одним и тем же путём» означает необходимость пройти все рёбра ровно один раз. Для существования эйлерова пути в связном графе достаточно, чтобы ровно две вершины имели нечётную степень. В данном плане именно два входа-выхода коридорной сети дают нечётные степени, остальные узлы имеют чётные степени, следовательно эйлеров путь существует и начинается в одной из нечётных вершин и заканчивается в другой. Формально: если числа нечётных вершин равно \(2\), то существует эйлеров путь; если \(0\), то существует эйлеров цикл; если больше \(2\), то эйлеров путь невозможен. Здесь выполняется \(2\).

Практическая трассировка: старт слева снизу на внешнем входе, движение по нижнему горизонтальному коридору к левым нижним ответвлениям с доставкой точки внизу слева, затем продолжение вдоль низа к центру и направо, посещая нижнюю центральную точку. Далее уход вправо к правой внешней стенке, поворот вверх по правому вертикальному коридору с поочередным заходом в правые боковые ответвления для двух правых точек. После правого подъёма переход по верхнему горизонтальному коридору налево, зайти в верхние карманы и доставить две верхние точки, не возвращаясь по уже пройденным рёбрам.

Затем спуститься в центральную область по вертикали, пройти внутренние ходы: сначала центральная верхняя точка, далее левый верхний карман, затем опуститься к левой средней точке, вернуться по непройденному участку к центральной нижней точке, и завершить выходом на левый верхний внешний проём, который является второй нечётной вершиной. Таким образом, все 9 пунктов посещены, каждое ребро пройдено ровно один раз, маршрут начинается на левом нижнем входе и заканчивается на левом верхнем выходе, что соответствует эйлерову пути по схеме и удовлетворяет условию задачи \(проход\;каждого\;ребра=1\) и \(повторов=\emptyset\).