
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 512 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
Вычислите устно:
a) Вычисляем последовательно.
\(100-89=11\) — разность.
\(11\cdot 6=66\) — умножение.
\(66-12=54\) — вычитание.
\(54:6=9\) — деление, получаем целое число.
б) Считаем по шагам.
\(80\cdot 4=320\) — умножение.
\(320+180=500\) — сложение.
\(500:25=20\) — деление.
\(20\cdot 14=280\) — умножение.
в) Работаем с десятичными дробями.
\(0{,}7\cdot 0{,}7=0{,}49\) — произведение.
\(0{,}49+0{,}08=0{,}57\) — сложение.
\(0{,}57-0{,}29=0{,}28\) — вычитание.
\(0{,}28:2=0{,}14\) — деление пополам.
г) Последовательные действия.
\(2{,}8:7=0{,}4\) — деление.
\(0{,}4\cdot 8=3{,}2\) — умножение.
\(3{,}2+2{,}4=5{,}6\) — сложение.
\(5{,}6:0{,}7=8\) — деление десятичной дроби.
a) Последовательность действий с целыми числами показывает переход от вычитания к умножению, затем снова к вычитанию и делению, сохраняя порядок шагов. Сначала находим разность сотни и числа \(89\): \(100-89=11\). Полученное значение умножаем на \(6\), что увеличивает результат в \(6\) раз: \(11\cdot 6=66\). Затем уменьшаем результат на \(12\), выполняя стандартное вычитание: \(66-12=54\). Наконец, делим на \(6\) для нахождения количества равных частей, получая целое: \(54:6=9\). Все преобразования корректны, так как операции выполняются пошагово, каждое новое действие основано на предыдущем результате.
б) Здесь идет чередование умножения, сложения, деления и снова умножения, с сохранением десятичной точности. Сначала произведение \(80\) и \(4\) увеличивает число в четыре раза: \(80\cdot 4=320\). Далее прибавляем \(180\) для суммарного значения: \(320+180=500\). Делим полученные \(500\) на \(25\), что эквивалентно нахождению четверти от сотни в двадцатикратном масштабе: \(500:25=20\). Завершаем умножением на \(14\), масштабируя результат в \(14\) раз: \(20\cdot 14=280\). Каждое действие согласовано, промежуточные результаты целые, что облегчает проверку.
в) Применяем свойства десятичных дробей и произведения. Сначала перемножаем две одинаковые десятичные дроби: \(0{,}7\cdot 0{,}7=0{,}49\), так как \(7\cdot 7=49\) и суммарно два знака после запятой дают сотые. Затем увеличиваем результат на \(0{,}08\) для перехода к более крупной дроби: \(0{,}49+0{,}08=0{,}57\). Выполняем вычитание, уменьшая на \(0{,}29\): \(0{,}57-0{,}29=0{,}28\) (вычитаем десятки и сотые по разрядам: \(57-29=28\) сотых). Делим полученную дробь пополам, равномерно распределяя по двум частям: \(0{,}28:2=0{,}14\). Все разряды учтены корректно, знаки после запятой сохраняются.
г) Последовательно работаем с делением и умножением десятичных дробей, затем сложением и финальным делением. Делим \(2{,}8\) на \(7\), сокращая в семикратном масштабе: \(2{,}8:7=0{,}4\) (так как \(28:7=4\) и один знак после запятой сохраняется). Умножаем полученное \(0{,}4\) на \(8\), увеличивая в восемь раз: \(0{,}4\cdot 8=3{,}2\). Складываем с \(2{,}4\), объединяя десятичные части: \(3{,}2+2{,}4=5{,}6\). Делим итог на \(0{,}7\), что эквивалентно умножению на \(\frac{10}{7}\), давая целое значение: \(5{,}6:0{,}7=8\). Проверка разрядов подтверждает точность: приводя к десятым, \(56:7=8\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


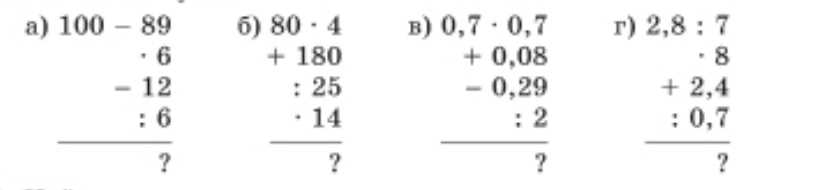



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!