
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 490 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
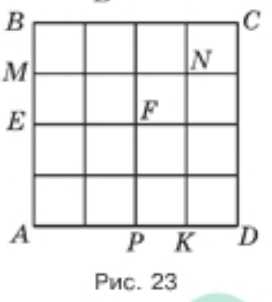
На рисунке 23 изображён квадрат \(ABCD\), разделённый на 16 равных частей. Определите по рисунку, какую часть составляет:
а) квадрат \(AEFP\) от квадрата \(ABCD\);
б) квадрат \(AEFP\) от квадрата \(AMNK\);
в) квадрат \(AMNK\) от квадрата \(ABCD\).
а) Площадь квадрата \(AEFP\) состоит из 4 маленьких квадратиков, а \(ABCD\) — из 16. Тогда отношение площадей: \(\frac{AEFP}{ABCD}=\frac{4}{16}=\frac{1}{4}\).
б) Площадь квадрата \(AEFP\) — 4 квадратика, а \(AMNK\) — 9. Отношение площадей: \(\frac{AEFP}{AMNK}=\frac{4}{9}\).
в) Площадь квадрата \(AMNK\) — 9 квадратиков, а \(ABCD\) — 16. Отношение площадей: \(\frac{AMNK}{ABCD}=\frac{9}{16}\).
а) Рассматриваем две фигуры: квадрат \(AEFP\) и квадрат \(ABCD\). Каждая их площадь измеряется числом равных маленьких квадратиков сетки. Площадь квадрата пропорциональна количеству таких единичных клеток, поэтому отношение площадей равно отношению соответствующих количеств клеток. По условию \(AEFP\) содержит 4 клеточки, а \(ABCD\) содержит 16 клеточек. Тогда отношение площадей находится делением: \(\frac{AEFP}{ABCD}=\frac{4}{16}\). Сократим дробь на 4: \(\frac{4}{16}=\frac{1}{4}\). Это означает, что площадь квадрата \(AEFP\) составляет четверть площади квадрата \(ABCD\), что согласуется с тем, что при одинаковой сетке количество клеток напрямую отражает площадь.
б) Теперь сравниваем квадраты \(AEFP\) и \(AMNK\). Метод тот же: считаем клетки, потому что единичные квадратики сетки одинаковы по размеру, и их число задаёт площадь каждой фигуры. По условию \(AEFP\) включает 4 клеточки, а \(AMNK\) включает 9 клеточек. Тогда отношение площадей равно \(\frac{AEFP}{AMNK}=\frac{4}{9}\). Эта дробь уже несократима, так как 4 и 9 не имеют общих делителей, кроме 1. Интерпретация: площадь \(AEFP\) составляет \(\frac{4}{9}\) площади \(AMNK\); если представить, что сторона квадрата связана с площадью как квадрат длины стороны, то увеличение числа клеток с 4 до 9 означает рост площади в \( \frac{9}{4} \) раза относительно \(AEFP\).
в) Сравниваем квадраты \(AMNK\) и \(ABCD\). Снова используем тот же принцип счёта клеток: площади равны количеству одинаковых единичных квадратиков. По условию \(AMNK\) состоит из 9 клеточек, а \(ABCD\) состоит из 16 клеточек. Отношение площадей равно \(\frac{AMNK}{ABCD}=\frac{9}{16}\). Эта дробь также несократима, поскольку 9 и 16 взаимно просты. Интерпретация: площадь квадрата \(AMNK\) составляет \(\frac{9}{16}\) площади квадрата \(ABCD\); поскольку площадь связана со стороной как квадрат стороны, отношение сторон этих квадратов будет \(\sqrt{\frac{9}{16}}=\frac{3}{4}\), что согласуется с тем, что при уменьшении стороны до \(\frac{3}{4}\) площади уменьшается до \(\frac{9}{16}\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!