ГДЗ по Математике 6 Класс Часть 1 Номер 466 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

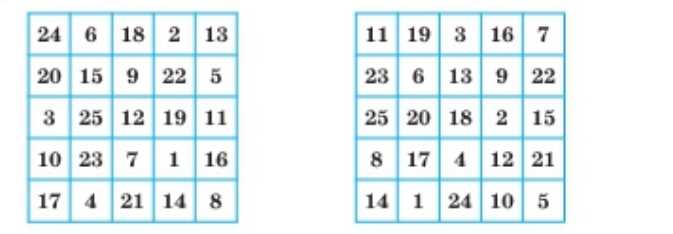
Кто быстрее? Найдите в таблице последовательно все числа от 1 до 25:

Решение: последовательно находим в каждой таблице числа от 1 до 25, двигаясь взглядом по строкам слева направо и сверху вниз, фиксируя найденное число и сразу переходя к следующему. Это тренировка внимания, вычислений нет.

Ответ: обе таблицы содержат полный набор чисел от 1 до 25; их можно найти устно по порядку \(1,2,\dots,25\), проходя клетки последовательно.

Решение: задача — тренировка зрительного поиска, где нужно по порядку найти числа от \(1\) до \(25\) в каждой из двух таблиц. Удобная практика: мысленно разбить поле на строки и столбцы, вести взгляд систематично, чтобы не возвращаться к уже просмотренным ячейкам. Начинаем с поиска \(1\): как только обнаружили \(1\), запоминаем ее позицию, затем переходим к \(2\), \(3\) и так далее до \(25\). Такой пошаговый метод снижает пропуски и ускоряет работу, потому что мозг переключается на один целевой паттерн за раз. Важно не перескакивать: просматриваем клетки слева направо, сверху вниз, а если число не найдено в текущей строке, продолжаем поиск в следующей. Когда число найдено, сразу сменяем цель на следующее, поддерживая последовательность \(1,2,\dots,25\).

Пояснение к стратегии: используем принцип фиксированной цели — в каждый момент времени ищем только одно число \(n\), где \(n\) последовательно принимает значения от \(1\) до \(25\). Когда \(n\) найдено, увеличиваем \(n\) на \(1\), то есть выполняем шаг \(n \rightarrow n+1\), пока не достигнем \(25\). Это можно описать кратко: начинаем с \(n=1\), повторяем цикл поиска, и завершаем, когда \(n=25\) найден. Такой подход устраняет лишние сравнения, потому что взгляд фильтрует сетку, выделяя только текущую цель. Если в строке отвлекают близкие по форме цифры (например, \(11\) рядом с \(1\)), применяем уточнение: сверяем разрядность и количество символов, чтобы избежать ошибок. При необходимости используем якорные точки — запоминаем расположение крайних чисел (например, \(1\), \(13\), \(25\)) как ориентиры, ускоряющие навигацию.

Итог: обе таблицы содержат полный набор чисел от \(1\) до \(25\), и их можно найти устно, последовательно от \(1\) до \(25\), двигаясь по сетке систематично. Процедура одинакова для обеих таблиц: выбираем число \(1\), затем последовательно \(2,3,\dots,25\), пока не будут отмечены все позиции. Вычислений нет, используется только внимание и методичный обход ячеек. Если на каком-то числе застряли, возвращаемся к систематическому просмотру строк или столбцов, поддерживая неизменный порядок \(1 \rightarrow 2 \rightarrow 3 \rightarrow \dots \rightarrow 25\), что гарантирует полный и корректный поиск.