ГДЗ по Математике 6 Класс Часть 1 Номер 464 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

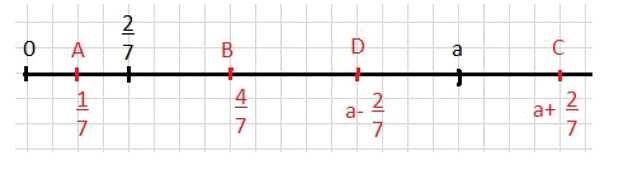
На координатном луче (рис. 20) отмечены дробь \(\frac{2}{7}\) и число \(a\). Покажите, где расположены на луче точки \(A\left(\frac{1}{7}\right)\), \(B\left(\frac{4}{7}\right)\), \(C\left(a + \frac{2}{7}\right)\), \(D\left(a — \frac{2}{7}\right)\).  

Точки \(A\left(\frac{1}{7}\right)\) и \(B\left(\frac{4}{7}\right)\) располагаются между \(0\) и \(\frac{2}{7}\) так: \(A\) левее, на расстоянии одной седьмой от нуля, \(B\) правее \(A\), на расстоянии четырёх седьмых от нуля.

Точки, связанные с \(a\): \(D\left(a-\frac{2}{7}\right)\) находится левее \(a\) на \(\frac{2}{7}\), а \(C\left(a+\frac{2}{7}\right)\) правее \(a\) на \(\frac{2}{7}\).

Точка \(A\left(\frac{1}{7}\right)\) располагается на координатном луче между \(0\) и \(\frac{2}{7}\). Так как \(\frac{1}{7}\) меньше \(\frac{2}{7}\), то \(A\) находится левее отмеченной доли \(\frac{2}{7}\) на расстоянии одной седьмой от нуля. Визуально это первая отметка после нуля: от \(0\) до \(A\) один равный шаг длины \(\frac{1}{7}\), а от \(A\) до \(\frac{2}{7}\) ещё один такой же шаг, что подтверждает соотношение \(\frac{1}{7}+\frac{1}{7}=\frac{2}{7}\).

Точка \(B\left(\frac{4}{7}\right)\) лежит правее и дальше от нуля, чем \(\frac{2}{7}\). Сравнение дробей показывает, что \(\frac{4}{7}>\frac{2}{7}\), следовательно, \(B\) расположена правее отметки \(\frac{2}{7}\) на расстояние \(\frac{2}{7}\). От нуля до \(B\) четыре равных шага по \(\frac{1}{7}\), то есть суммарно \(\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}=\frac{4}{7}\). Поэтому порядок точек слева направо на первом участке таков: \(0\), затем \(A\left(\frac{1}{7}\right)\), далее \(\frac{2}{7}\), и правее их \(B\left(\frac{4}{7}\right)\).

Для точек, связанных с числом \(a\), используем правило смещения на луче: прибавление положительной дроби сдвигает точку вправо, вычитание — влево. Тогда \(C\left(a+\frac{2}{7}\right)\) находится правее \(a\) на длину отрезка \(\frac{2}{7}\). Геометрически это означает, что если от отметки \(a\) сделать два последовательных шага по \(\frac{1}{7}\), мы попадём в \(C\), поскольку \(\frac{2}{7}=\frac{1}{7}+\frac{1}{7}\). Напротив, \(D\left(a-\frac{2}{7}\right)\) располагается левее \(a\) на ту же величину \(\frac{2}{7}\): от \(a\) выполняем два шага по \(\frac{1}{7}\) влево и получаем положение \(D\). Таким образом, относительный порядок этих трёх отметок всегда: \(D\left(a-\frac{2}{7}\right)\) слева, затем \(a\), и правее \(C\left(a+\frac{2}{7}\right)\); расстояния \(aD\) и \(aC\) равны \(\frac{2}{7}\).