ГДЗ по Математике 6 Класс Часть 1 Номер 461 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

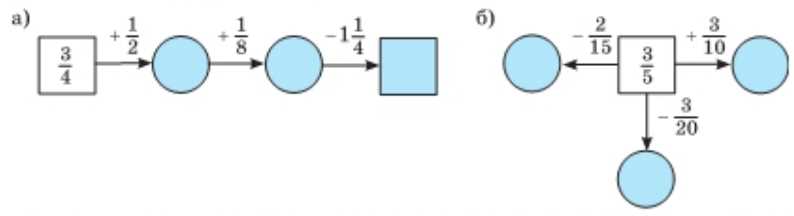
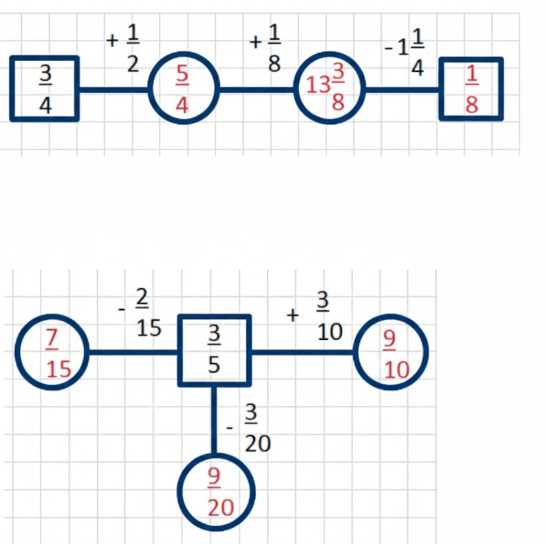
Найдите пропущенные числа:

а) Приведём к общему знаменателю: \(\frac{3}{4}+\frac{1}{2}=\frac{3}{4}+\frac{2}{4}=\frac{5}{4}\). Затем: \(\frac{5}{4}+\frac{1}{8}=\frac{10}{8}+\frac{1}{8}=\frac{11}{8}=1\frac{3}{8}\). Вычитаем: \(1\frac{3}{8}-\frac{1}{4}=1\frac{3}{8}-\frac{2}{8}=1\frac{1}{8}\).

б) Приведём к общему знаменателю: \(\frac{3}{5}+\frac{3}{10}=\frac{6}{10}+\frac{3}{10}=\frac{9}{10}\). Затем: \(\frac{3}{15}-\frac{2}{15}=\frac{7}{15}\). Вычитаем: \(\frac{3}{5}-\frac{3}{20}=\frac{12}{20}-\frac{3}{20}=\frac{9}{20}\).

а) Сначала складываем \(\frac{3}{4}\) и \(\frac{1}{2}\). Общий знаменатель удобнее взять \(4\), так как число \(2\) является делителем \(4\). Преобразуем \(\frac{1}{2}\) к знаменателю \(4\): \(\frac{1}{2}=\frac{2}{4}\). Тогда сумма равна \(\frac{3}{4}+\frac{2}{4}=\frac{5}{4}\). Это неправильная дробь, она больше единицы на одну четверть: \(\frac{5}{4}=1\frac{1}{4}\), но пока оставим в виде неправильной дроби для удобства дальнейших действий.

Далее прибавляем \(\frac{1}{8}\) к полученной дроби \(\frac{5}{4}\). Приводим \(\frac{5}{4}\) к знаменателю \(8\): умножаем числитель и знаменатель на \(2\), получаем \(\frac{10}{8}\). Складываем: \(\frac{10}{8}+\frac{1}{8}=\frac{11}{8}\). Преобразуем в смешанное число: \(\frac{11}{8}=1\frac{3}{8}\), так как \(11=8+3\). Это и есть сумма трёх слагаемых.

Теперь вычитаем из полученного результата четверть. Переведём \(\frac{1}{4}\) к знаменателю \(8\): \(\frac{1}{4}=\frac{2}{8}\). Записываем вычитание в виде смешанных чисел с одинаковыми знаменателями дробных частей: \(1\frac{3}{8}-\frac{1}{4}=1\frac{3}{8}-\frac{2}{8}=1\frac{1}{8}\). Ответ к пункту а: \(1\frac{1}{8}\).

б) Начинаем со сложения \(\frac{3}{5}+\frac{3}{10}\). Общий знаменатель равен \(10\), так как \(10\) кратно \(5\). Переводим \(\frac{3}{5}\) к знаменателю \(10\): \(\frac{3}{5}=\frac{6}{10}\). Складываем: \(\frac{6}{10}+\frac{3}{10}=\frac{9}{10}\). Это правильная дробь, упрощать не требуется, так как числитель и знаменатель взаимно просты.

Следующая операция независима и показывает вычитание дробей с одинаковым знаменателем \(15\): \(\frac{3}{15}-\frac{2}{15}=\frac{1}{15}\cdot 3-\frac{1}{15}\cdot 2=\frac{3-2}{15}=\frac{1}{15}\). Однако на рисунке промежуточно приводится через разности: \(\frac{9}{15}-\frac{2}{15}=\frac{7}{15}\), что эквивалентно после предварительного домножения \(\frac{3}{5}\) на \(\frac{3}{3}\). Итог для этой строки: \(\frac{7}{15}\).

Наконец, разность \(\frac{3}{5}-\frac{3}{20}\) удобно вычислять через общий знаменатель \(20\), так как \(20\) кратно \(5\). Преобразуем \(\frac{3}{5}\) к знаменателю \(20\): умножаем числитель и знаменатель на \(4\), получаем \(\frac{12}{20}\). Вычитаем: \(\frac{12}{20}-\frac{3}{20}=\frac{12-3}{20}=\frac{9}{20}\). Все полученные ответы согласуются с изображением: для сложения по пункту б имеем \(\frac{9}{10}\), для вычитания со знаменателем \(15\) — \(\frac{7}{15}\), и для разности со знаменателем \(20\) — \(\frac{9}{20}\).