
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 42 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
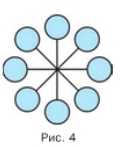
Какие различные натуральные числа надо вписать в кружки (рис. 4), чтобы произведение каждых двух чисел, помещённых в кружках, соединённых отрезком, равнялось 70? Подумайте, как можно назвать набор чисел, оказавшихся в кружках.
В кружках нужно вписать делители числа 70, такие что произведение чисел в соседних кружках равно 70.
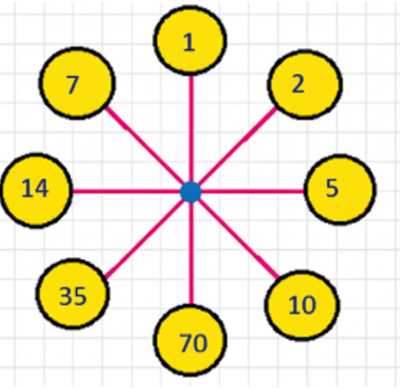
Числа: 1, 2, 5, 7, 10, 14, 35, 70.
Это множество делителей числа 70.
Каждая пара соседних чисел \(a\) и \(b\) удовлетворяет условию \(a \times b = 70\).
Набор чисел в кружках — это делители числа 70.
Для решения задачи нужно понять, какие числа можно вписать в кружки так, чтобы произведение чисел в двух соседних кружках было равно 70. Это означает, что если два кружка соединены линией, и в них стоят числа \(a\) и \(b\), то должно выполняться равенство \(a \times b = 70\).
Число 70 имеет несколько делителей — натуральных чисел, на которые 70 делится без остатка. Чтобы найти все делители 70, нужно разложить его на простые множители: \(70 = 2 \times 5 \times 7\). Теперь, используя эти множители, можно составить все возможные делители, перемножая их в разных комбинациях. Делителями числа 70 являются числа 1, 2, 5, 7, 10, 14, 35 и 70. Именно эти числа и нужно вписать в кружки.
Пары чисел, соединённых линиями, — это такие делители, произведение которых равно 70. Например, 1 и 70, 2 и 35, 5 и 14, 7 и 10. Таким образом, каждое число из множества делителей 70 связано с другим числом так, что их произведение равно 70. Набор чисел, вписанных в кружки, называется множеством делителей числа 70. Это множество содержит все числа, на которые 70 делится без остатка, и которые удовлетворяют условию произведения соседних чисел, равного 70.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!