ГДЗ по Математике 6 Класс Часть 1 Номер 393 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

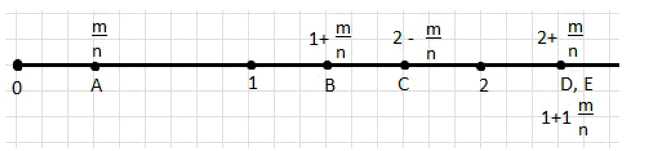
На координатном луче отмечена точка \(A\left(\frac{m}{n}\right)\) (рис. 17). Отметьте на луче точки, координаты которых равны:
а) \(1 + \frac{m}{n}\); б) \(2 — \frac{m}{n}\); в) \(2 + \frac{m}{n}\); г) \(1 + \frac{1}{m}\frac{m}{n}\).

а) \(1 + \frac{m}{n} = B\). Точка с координатой \(1 + \frac{m}{n}\) отмечена на луче как \(B\).

б) \(2 — \frac{m}{n} = C\). Точка с координатой \(2 — \frac{m}{n}\) отмечена на луче как \(C\).

в) \(2 + \frac{m}{n} = D\). Точка с координатой \(2 + \frac{m}{n}\) отмечена на луче как \(D\).

г) \(1 + 1 \cdot \frac{m}{n} = 1 + \frac{m}{n} = E\). Точка с координатой \(1 + \frac{m}{n}\) отмечена на луче как \(E\).

Таким образом, точки с координатами из условий а) и г) совпадают и обозначены как \(B\) и \(E\) соответственно.

а) Точка \(A\) имеет координату \(\frac{m}{n}\) на числовой оси. Чтобы найти точку с координатой \(1 + \frac{m}{n}\), нужно к числу 1 прибавить значение \(\frac{m}{n}\). Это означает, что мы сдвигаемся вправо от точки 1 на расстояние \(\frac{m}{n}\). На рисунке эта точка обозначена как \(B\), так как именно там расположена координата \(1 + \frac{m}{n}\).

б) Для точки с координатой \(2 — \frac{m}{n}\) мы начинаем от числа 2 и вычитаем \(\frac{m}{n}\). Это сдвиг влево от точки 2 на величину \(\frac{m}{n}\). Следовательно, точка \(C\) на оси находится между 1 и 2, ближе к 2, и именно ей соответствует координата \(2 — \frac{m}{n}\).

в) Точка с координатой \(2 + \frac{m}{n}\) находится правее числа 2, так как к 2 прибавляется положительное число \(\frac{m}{n}\). Это сдвиг вправо от 2 на \(\frac{m}{n}\). На рисунке точка \(D\) отмечена именно в этом месте, что соответствует координате \(2 + \frac{m}{n}\).

г) Выражение \(1 + 1 \cdot \frac{m}{n}\) упрощается до \(1 + \frac{m}{n}\), так как умножение на 1 не меняет значение. Значит, координата точки \(E\) совпадает с координатой точки \(B\), то есть \(1 + \frac{m}{n}\). На числовой оси эти две точки совпадают, что и отражено на рисунке.

Таким образом, каждая точка на числовой оси соответствует своему выражению: \(B = 1 + \frac{m}{n}\), \(C = 2 — \frac{m}{n}\), \(D = 2 + \frac{m}{n}\), а \(E\) совпадает с \(B\) и имеет координату \(1 + \frac{m}{n}\). Это подтверждается расположением точек на оси в соответствии с арифметическими операциями сложения и вычитания с дробью \(\frac{m}{n}\).