
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 35 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
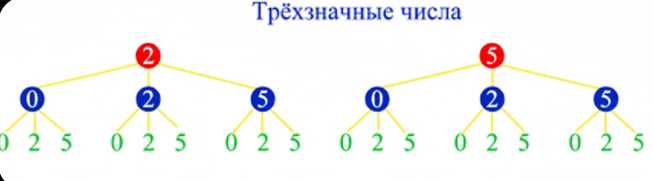
Напишите множество трёхзначных чисел, в запись которых входят лишь цифры 0, 2, 5 и которые:
а) делятся на 2;
б) делятся на 5.
а) Чтобы число делилось на 2, оно должно быть чётным, то есть оканчиваться на 0, 2.
200, 202, 220, 222, 250, 252, 500, 502, 520, 522, 550, 552.
б) Чтобы число делилось на 5, оно должно оканчиваться на 0 или 5.
200, 205, 220, 225, 250, 255, 500, 505, 520, 525, 550, 555.
а) Для того чтобы трёхзначное число делилось на 2, оно обязательно должно быть чётным. Чётные числа — это такие числа, которые заканчиваются на одну из цифр: 0, 2, 4, 6 или 8. В нашем случае числа строятся из цифр 0, 2, 5, поэтому среди них чётными будут только те, которые заканчиваются на 0 или 2. При переборе всех возможных комбинаций трёхзначных чисел из данных цифр, учитываем, что первая цифра не может быть 0 (иначе получится двузначное число). Остальные цифры могут быть любыми из набора 0, 2, 5. Таким образом, получаем следующие числа: 200, 202, 220, 222, 250, 252, 500, 502, 520, 522, 550, 552. Все эти числа заканчиваются на 0 или 2, то есть они чётные и делятся на 2.
б) Для того чтобы трёхзначное число делилось на 5, оно должно оканчиваться на 0 или 5. Это правило связано с тем, что любое число, заканчивающееся на 0 или 5, делится на 5 без остатка. В нашем наборе допустимых цифр для последнего разряда есть 0 и 5, поэтому перебираем все возможные варианты, где последняя цифра — 0 или 5. Первая цифра снова не может быть 0, чтобы число оставалось трёхзначным. Остальные цифры могут быть любыми из предложенных вариантов. В результате получаем числа: 200, 205, 220, 225, 250, 255, 500, 505, 520, 525, 550, 555.
Все перечисленные числа соответствуют условиям задачи: в пункте а) они оканчиваются на чётную цифру, а в пункте б) — на 0 или 5, что гарантирует делимость на 2 и 5 соответственно. При составлении перечня важно внимательно следить за тем, чтобы первая цифра была отлична от 0, а остальные могли принимать любое значение из набора, указанного в условии. Формально, если число записано как \(abc\), где \(a, b, c\) — цифры, то для делимости на 2 верно: \(c = 0\) или \(c = 2\); для делимости на 5: \(c = 0\) или \(c = 5\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!