
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 325 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
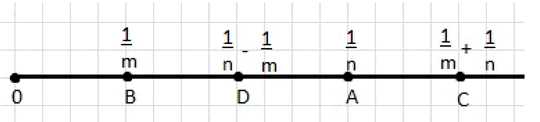
На координатном луче отмечены точки \(A\left(\frac{1}{n}\right)\) и \(B\left(\frac{1}{m}\right)\) (рис. 16).
Отметьте на луче точку с координатами:
а) \(\frac{1}{m} + \frac{1}{n}\); б) \(\frac{1}{n} — \frac{1}{m}\).
а) \( \frac{1}{m} + \frac{1}{n} = C \).
б) \( \frac{1}{n} — \frac{1}{m} = D \).
а) Рассмотрим выражение \( \frac{1}{m} + \frac{1}{n} = C \). Здесь \( m \) и \( n \) — числа, для которых мы берём обратные значения, а затем складываем их. Сумма этих дробей равна некоторой константе \( C \). Чтобы понять это равенство, важно заметить, что каждая дробь представляет собой расстояние от нуля до точки на числовой оси, обозначенной как \( \frac{1}{m} \) и \( \frac{1}{n} \). Сумма этих значений показывает, что точка \( C \) на оси находится на расстоянии, равном сумме этих двух отрезков. Таким образом, \( C \) — это сумма двух положительных величин, каждая из которых обратна соответствующему числу.
б) В выражении \( \frac{1}{n} — \frac{1}{m} = D \) происходит вычитание обратных значений. Здесь мы берём дробь \( \frac{1}{n} \) и вычитаем из неё дробь \( \frac{1}{m} \). Результат равен некоторой величине \( D \), которая может быть как положительной, так и отрицательной, в зависимости от того, какое из чисел \( m \) или \( n \) больше. Если \( n > m \), то \( D \) положительно, иначе отрицательно. Это выражение отражает разницу между двумя расстояниями на числовой оси.
На рисунке показано расположение точек на числовой оси: \( 0 \), \( \frac{1}{m} \), \( \frac{1}{n} \), а также точки \( B, D, A, C \), которые соответствуют суммам и разностям этих дробей. Например, точка \( C \) находится на расстоянии \( \frac{1}{m} + \frac{1}{n} \) от нуля, что соответствует сумме в пункте а). Точка \( D \) соответствует разности \( \frac{1}{n} — \frac{1}{m} \) из пункта б). Таким образом, графическое изображение иллюстрирует, как складываются и вычитаются дроби, показывая визуально результат этих операций на числовой оси.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!