
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 317 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
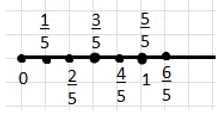
Запишите все дроби со знаменателем 5, большие, чем \(\frac{1}{5}\), и меньшие, чем \(\frac{6}{5}\). Отметьте эти дроби на координатном луче.
\( \frac{1}{5} < \frac{x}{5} < \frac{6}{5} \)
\( x = \{2; 3; 4; 5\} \)
Дроби:
\( \frac{2}{5}; \frac{3}{5}; \frac{4}{5}; \frac{5}{5} \)
Рассмотрим неравенство \( \frac{1}{5} < \frac{x}{5} < \frac{6}{5} \). Здесь переменная \( x \) находится в числителе дроби с фиксированным знаменателем 5. Чтобы понять, какие значения может принимать \( x \), нужно проанализировать, при каких числах \( x \) дробь \( \frac{x}{5} \) будет строго больше \( \frac{1}{5} \) и строго меньше \( \frac{6}{5} \).
Поскольку знаменатель у всех дробей одинаковый и равен 5, сравнение можно свести к сравнению числителей. Из неравенства следует, что \( 1 < x < 6 \). При этом \( x \) принимает только целочисленные значения из множества \( \{2; 3; 4; 5\} \), так как они удовлетворяют условию. Значения \( x = 1 \) или \( x = 6 \) не подходят, потому что неравенство строгое, то есть равенства быть не должно.
Для каждого из найденных значений \( x \) можно записать соответствующую дробь: \( \frac{2}{5}, \frac{3}{5}, \frac{4}{5}, \frac{5}{5} \). Эти дроби находятся на числовой оси между \( \frac{1}{5} \) и \( \frac{6}{5} \). На рисунке видно, что эти точки действительно лежат между указанными границами, что подтверждает правильность решения. Таким образом, множество подходящих дробей — это именно дроби с числителем из множества \( \{2; 3; 4; 5\} \) и знаменателем 5.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!