
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 25 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
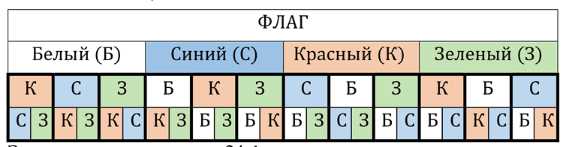
Сколько существует флагов, составленных из трёх горизонтальных полос одинаковой ширины и различных цветов — белого, зелёного, красного и синего? Есть ли среди этих флагов Государственный флаг Российской Федерации?
Пусть имеется 4 цвета: белый, синий, красный, зелёный. Флаг состоит из трёх полос, причём полосы должны быть разного цвета.
Для верхней полосы есть 4 варианта. Для второй полосы — 3 варианта (любой, кроме цвета верхней полосы). Для третьей полосы — 2 варианта (любой, кроме двух предыдущих).
Итого: \(4 \times 3 \times 2 = 24\) варианта.
Среди них есть флаг РФ — белый, синий, красный.
Рассмотрим задачу более подробно. Пусть имеется 4 цвета: белый (Б), синий (С), красный (К), зелёный (З). Флаг состоит из трёх полос, причём все полосы должны быть разного цвета, то есть цвета не повторяются. Для каждой полосы будем поочерёдно выбирать цвет, учитывая, что каждый следующий цвет не должен совпадать с предыдущим.
Для верхней полосы выбор не ограничен: можно взять любой из 4 цветов. После выбора верхнего цвета для второй полосы остаётся только 3 варианта, так как второй цвет не должен совпадать с первым. После выбора первых двух цветов для третьей полосы остаётся 2 варианта, потому что третий цвет не должен совпадать ни с первым, ни со вторым.
Таким образом, общее количество способов составить флаг из трёх разных цветов определяется формулой: \(4 \times 3 \times 2 = 24\). Это можно объяснить тем, что для каждой из 4 возможных верхних полос есть по 3 варианта второй полосы и по 2 варианта третьей полосы. Если бы полосы могли быть одинакового цвета, то вариантов было бы \(4^{3}\), но по условию задачи цвета должны различаться, поэтому мы используем перемножение по принципу последовательного выбора без повторений.
Среди этих 24 вариантов обязательно присутствует флаг РФ — белый, синий, красный (в любом порядке, но если требуется именно порядок: белый сверху, синий посередине, красный внизу). Это соответствует одному из вариантов из перечисленных комбинаций. Ответ: \(24\) варианта, среди них есть флаг РФ.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!