
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 24 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
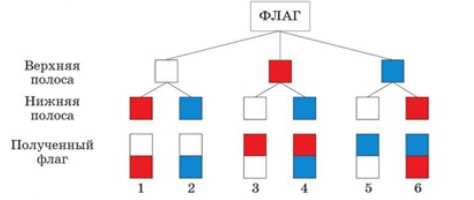
Государственные флаги многих стран состоят из горизонтальных или вертикальных полос разных цветов. Сколько могло бы быть различных государственных флагов, состоящих из двух горизонтальных полос одинаковой ширины и разного цвета — белого, красного и синего?
Пусть верхняя полоса может быть белой, красной или синей — всего 3 варианта. Для каждой верхней полосы нижняя может быть любым из двух оставшихся цветов. Значит, число вариантов: \(3 \times 2 = 6\).
Перечислим варианты:
1. Верхняя — белая, нижняя — красная
2. Верхняя — белая, нижняя — синяя
3. Верхняя — красная, нижняя — белая
4. Верхняя — красная, нижняя — синяя
5. Верхняя — синяя, нижняя — белая
6. Верхняя — синяя, нижняя — красная
Для решения задачи сначала определим, сколько всего цветов можно использовать для полос флага. По условию это три цвета: белый, красный и синий. Флаг состоит из двух горизонтальных полос одинаковой ширины, причём полосы должны быть разного цвета. Это значит, что одна и та же комбинация цветов, расположенных в разном порядке, будет считаться разными вариантами флага.
Рассмотрим выбор цвета для верхней полосы. У нас есть три варианта: белый, красный или синий. После того как выбран цвет верхней полосы, для нижней полосы остаётся только два варианта, потому что она должна отличаться от верхней. Например, если верхняя полоса белая, то нижняя может быть либо красной, либо синей. Аналогично, если верхняя красная, нижняя может быть белой или синей, и если верхняя синяя, нижняя может быть белой или красной. Таким образом, для каждого из трёх вариантов верхней полосы есть по два варианта нижней полосы. Количество всех возможных флагов вычисляется по формуле комбинаторики: \(3 \times 2 = 6\).
Запишем все возможные варианты флагов, чтобы убедиться, что ни один не пропущен:
1. Верхняя — белая, нижняя — красная
2. Верхняя — белая, нижняя — синяя
3. Верхняя — красная, нижняя — белая
4. Верхняя — красная, нижняя — синяя
5. Верхняя — синяя, нижняя — белая
6. Верхняя — синяя, нижняя — красная
Если бы полосы могли быть одного цвета, то количество вариантов увеличилось бы, но по условию задачи такие варианты не рассматриваются. Задача относится к разделу математики — комбинаторике, который изучает способы выбора и размещения объектов. В данном случае мы использовали правило произведения: если одно действие можно выполнить \(n\) способами, а другое — \(m\) способами, то оба действия вместе можно выполнить \(n \times m\) способами. Здесь \(3\) варианта для верхней полосы и \(2\) варианта для нижней, итого \(3 \times 2 = 6\) вариантов.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!