ГДЗ по Математике 6 Класс Часть 1 Номер 234 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

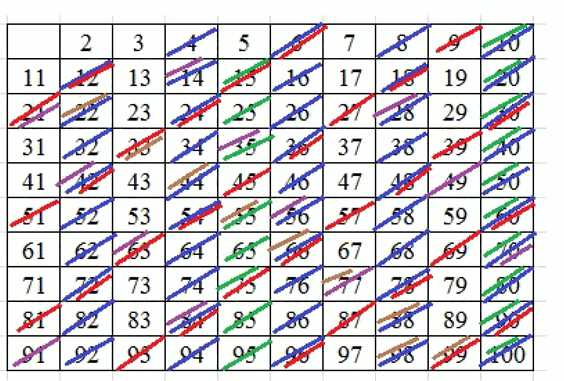
Найдите методом «решета Эратосфена» все простые числа среди первых ста натуральных чисел.

Записываем числа от 2 до 100.

Последовательно вычеркиваем кратные: сначала 2 (кроме 2), затем 3 (кроме 3), потом 5 (кроме 5), далее 7 и 11 (кроме 7 и 11).

Остаются простые числа:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Метод основан на решете Эратосфена: записываем натуральные числа от 2 до 100 и по шагам удаляем составные, которые имеют нетривиальные делители. На первом шаге оставляем 2 и вычеркиваем все кратные 2: это числа вида \(2k\) при \(k\geq 2\), то есть \(4,6,8,\dots,100\). На втором шаге оставляем 3 и вычеркиваем кратные 3: числа вида \(3k\) при \(k\geq 2\), например \(6,9,12,\dots,99\). При пересечении множеств кратных некоторые уже удалены на предыдущем шаге, что нормально: составные могут иметь несколько простых делителей. На третьем шаге работаем с 5: оставляем 5 и удаляем все \(5k\) при \(k\geq 2\), то есть \(10,15,20,\dots,100\). Далее аналогично для 7 и 11: сохраняем 7 и 11, удаляя \(7k\) и \(11k\) при \(k\geq 2\), то есть \(14,21,28,\dots,98\) и \(22,33,44,\dots,99\). Эти шаги достаточны, поскольку проверка делителей до \(\sqrt{100}=10\) гарантирует, что любое составное число до 100 имеет делитель среди \(2,3,5,7\). Число 11 используется как дополнительная демонстрация: его кратные \(11k\) при \(k\geq 2\) лежат в диапазоне до 99 и уже покрываются предыдущими шагами, но явное вычеркивание сохраняет наглядность.

Идея корректности такова: если число \(n\) составное, то существует простой делитель \(p\) с \(p\leq \sqrt{n}\). Поэтому, удалив все кратные простым \(p\) с \(p\leq \sqrt{100}\), мы устраняем все составные в диапазоне. Числа, которые не удалены, не имеют делителей, кроме 1 и себя, то есть являются простыми по определению. Например, число 37 остаётся, поскольку ни один из делителей \(2,3,5,7\) его не делит: \(37\bmod 2=1\), \(37\bmod 3=1\), \(37\bmod 5=2\), \(37\bmod 7=2\). Аналогично, 97 остаётся, так как \(97>\sqrt{100}\), и проверка делителей до 10 подтверждает отсутствие делителей.

Итоговый список незачёркнутых чисел, то есть простых в диапазоне от 2 до 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. Эти числа удовлетворяют определению простоты: для каждого \(p\) из списка любые делители кроме 1 и самого \(p\) отсутствуют, что видно из того, что при делении на любой \(q\in\{2,3,5,7\}\) получаем ненулевые остатки и что потенциальные делители \(q>7\) не нужны для проверки в этом диапазоне, поскольку \(q^{2}>100\).