ГДЗ по Математике 6 Класс Часть 1 Номер 220 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

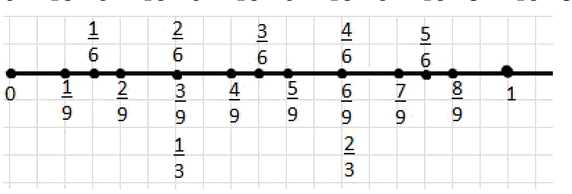
 Начертите координатный луч, приняв за единичный отрезок 18 клеток тетради. Отметьте на координатном луче точки с координатами , . 46 9 5 0 1. 2 01 6 1. 2. Какие из этих чисел изображаются на координатном луче одной и той же точкой? Запишите соответствующие равенства.

1) Переведём все данные координаты к долям единичного отрезка, где 1 единица = 18 клеток. Тогда точки на луче совпадут, если числа равны как дроби с знаменателем 18.

2) Приведём к общему знаменателю 18:
— \( \frac{1}{9}=\frac{2}{18} \), \( \frac{2}{9}=\frac{4}{18} \), \( \frac{3}{9}=\frac{6}{18} \), \( \frac{4}{9}=\frac{8}{18} \), \( \frac{5}{9}=\frac{10}{18} \), \( \frac{6}{9}=\frac{12}{18} \), \( \frac{7}{9}=\frac{14}{18} \), \( \frac{8}{9}=\frac{16}{18} \).
— \( \frac{1}{6}=\frac{3}{18} \), \( \frac{2}{6}=\frac{6}{18} \), \( \frac{3}{6}=\frac{9}{18} \), \( \frac{4}{6}=\frac{12}{18} \), \( \frac{5}{6}=\frac{15}{18} \).
— \( \frac{1}{3}=\frac{6}{18} \), \( \frac{2}{3}=\frac{12}{18} \).

3) Итоговые равенства совпадающих точек:
\( \frac{1}{9}=\frac{2}{18} \);
\( \frac{2}{9}=\frac{4}{18} \);
\( \frac{3}{9}=\frac{6}{18} \);
\( \frac{4}{9}=\frac{8}{18} \);
\( \frac{5}{9}=\frac{10}{18} \);
\( \frac{6}{9}=\frac{12}{18} \);
\( \frac{7}{9}=\frac{14}{18} \);
\( \frac{8}{9}=\frac{16}{18} \);
\( \frac{1}{6}=\frac{3}{18} \);
\( \frac{2}{6}=\frac{6}{18} \);
\( \frac{3}{6}=\frac{9}{18} \);
\( \frac{4}{6}=\frac{12}{18} \);
\( \frac{5}{6}=\frac{15}{18} \);
\( \frac{1}{3}=\frac{6}{18} \);
\( \frac{2}{3}=\frac{12}{18} \).

Принимаем единичный отрезок равным 18 клеткам: это значит, что каждая точка с координатой \(x\) на луче соответствует длине в \(x\) долей от 18 клеток. Чтобы понять, какие числа изображаются одной точкой, удобно все данные дроби привести к знаменателю 18. Тогда совпадение координат будет видно напрямую: если две дроби имеют одинаковый числитель при знаменателе 18, они задают одно и то же положение точки на луче. Например, дробь \( \frac{1}{9} \) означает одну девятую от единицы; так как единица — это 18 клеток, одна девятая от неё равна \( \frac{18}{9}=2 \) клеткам, то есть \( \frac{1}{9}=\frac{2}{18} \). Аналогично, для шестых: \( \frac{1}{6} \) от единицы — это \( \frac{18}{6}=3 \) клетки, значит \( \frac{1}{6}=\frac{3}{18} \). Этот приём масштабирования — умножение числителя и знаменателя на одно и то же число — не меняет значение дроби и переводит её к общей «линейке» в 18 долей, где легко сравнивать.

Проведём такую операцию для всех предложенных дробей. Для девятых умножаем на 2: \( \frac{1}{9}=\frac{2}{18} \), \( \frac{2}{9}=\frac{4}{18} \), \( \frac{3}{9}=\frac{6}{18} \), \( \frac{4}{9}=\frac{8}{18} \), \( \frac{5}{9}=\frac{10}{18} \), \( \frac{6}{9}=\frac{12}{18} \), \( \frac{7}{9}=\frac{14}{18} \), \( \frac{8}{9}=\frac{16}{18} \). Для шестых умножаем на 3: \( \frac{1}{6}=\frac{3}{18} \), \( \frac{2}{6}=\frac{6}{18} \), \( \frac{3}{6}=\frac{9}{18} \), \( \frac{4}{6}=\frac{12}{18} \), \( \frac{5}{6}=\frac{15}{18} \). Для третьих умножаем на 6: \( \frac{1}{3}=\frac{6}{18} \), \( \frac{2}{3}=\frac{12}{18} \). Теперь видно, какие пары совпадают: каждая пара с одинаковой записью при знаменателе 18 даёт одну и ту же точку. Например, \( \frac{2}{6} \), \( \frac{3}{9} \) и \( \frac{1}{3} \) все равны \( \frac{6}{18} \), значит изображаются одной точкой на луче; аналогично \( \frac{4}{6} \), \( \frac{6}{9} \) и \( \frac{2}{3} \) равны \( \frac{12}{18} \).

Запишем соответствующие равенства совпадающих точек, сгруппировав их по одинаковым координатам в долях от 18 клеток: \( \frac{1}{9}=\frac{2}{18} \); \( \frac{2}{9}=\frac{4}{18} \); \( \frac{3}{9}=\frac{6}{18} \); \( \frac{4}{9}=\frac{8}{18} \); \( \frac{5}{9}=\frac{10}{18} \); \( \frac{6}{9}=\frac{12}{18} \); \( \frac{7}{9}=\frac{14}{18} \); \( \frac{8}{9}=\frac{16}{18} \); \( \frac{1}{6}=\frac{3}{18} \); \( \frac{2}{6}=\frac{6}{18} \); \( \frac{3}{6}=\frac{9}{18} \); \( \frac{4}{6}=\frac{12}{18} \); \( \frac{5}{6}=\frac{15}{18} \); \( \frac{1}{3}=\frac{6}{18} \); \( \frac{2}{3}=\frac{12}{18} \). Таким образом, совпадения видны: \( \frac{2}{6}=\frac{3}{9}=\frac{1}{3}=\frac{6}{18} \) и \( \frac{4}{6}=\frac{6}{9}=\frac{2}{3}=\frac{12}{18} \); остальные равенства показывают эквивалентные записи тех же точек относительно масштаба из 18 долей.