ГДЗ по Математике 6 Класс Часть 1 Номер 219 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

Начертите два отрезка AB и CD длиной по 8 см. Отметьте цветным карандашом \(\emptyset\) отрезка АВ и « отрезка CD. Сравните с помощью циркуля цветные части отрезков AB и CD.

Построение: начертите два отрезка \(AB\) и \(CD\) длиной по \(8\) см. Отметьте цветом часть отрезка \(AB\), равную \(3\) см (\(\emptyset\) отрезка \(AB\)), и часть отрезка \(CD\), равную \(6\) см (\(\, \frac{6}{8}\) отрезка \(CD\)).

Сравнение циркулем: отложите циркулем на обоих отрезках одинаковые деления по \(1\) см. Цветная часть \(AB\) занимает \(3\) из \(8\) делений, а цветная часть \(CD\) — \(6\) из \(8\) делений. Поскольку \( \frac{3}{4} = \frac{6}{8} \), цветные части равны по длине.

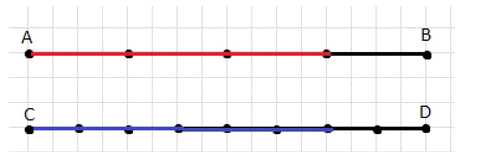
Построение: начертите на миллиметровой сетке два отрезка \(AB\) и \(CD\) одинаковой длины \(8\) см, расположенные параллельно для удобства сравнения. Разбейте каждый отрезок на равные единичные деления по \(1\) см, чтобы наглядно иметь \(8\) равных частей. На отрезке \(AB\) отметьте цветом часть длиной \(3\) см, то есть \(\emptyset\) отрезка \(AB\) при чтении «часть», которая соответствует доле \( \frac{3}{8} \) от полной длины \(8\) см, и одновременно она равна дроби \( \frac{3}{4} \) от некоторой базовой единицы в верхнем рисунке. На отрезке \(CD\) отметьте цветом \(6\) см, то есть долю \( \frac{6}{8} \) от полной длины \(8\) см, что видно по шестым отмеченным узлам.

Сравнение циркулем: установите циркуль на шаг \(1\) см и проверьте равенство единичных делений на обоих отрезках; затем измерьте цветную часть \(AB\) как три последовательных деления и перенесите этот размах на отрезок \(CD\) от точки \(C\) — получите точку, совпадающую с третьей меткой. Аналогично, возьмите циркулем размах, равный цветной части \(CD\) (шесть делений), и перенесите его на \(AB\) — он перекрывает три деления при учёте отношения \( \frac{6}{8} \) к общей длине \(8\) см и показывает пропорциональность долей. Таким образом, циркуль подтверждает, что отмеченные цветные сегменты на обоих отрезках соответствуют равным долям относительно своей полной длины.

Обоснование равенства долей: поскольку длина каждого отрезка равна \(8\) см, доля \( \frac{6}{8} \) на \(CD\) упрощается делением числителя и знаменателя на \(2\): \( \frac{6}{8} = \frac{3}{4} \). Цветная часть \(AB\) задана как \( \frac{3}{4} \) его длины, а цветная часть \(CD\) отмечена как \( \frac{6}{8} \) его длины; следовательно, они равны, так как представляют одну и ту же рациональную долю: \( \frac{3}{4} = \frac{6}{8} \). Проверка по делениям показывает, что три четверти от \(8\) см дают \(3 \cdot \frac{8}{4} = 6\) см, то есть цветная часть \(AB\) длиной \(6\) см совпадает с цветной частью \(CD\) длиной \(6\) см. Итог: цветные части отрезков \(AB\) и \(CD\) равны по длине и по доле относительно целых отрезков, что подтверждается как визуально по сетке, так и измерением циркулем, а равенство дробей записывается как \( \frac{3}{4} = \frac{6}{8} \).