ГДЗ по Математике 6 Класс Часть 1 Номер 216 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

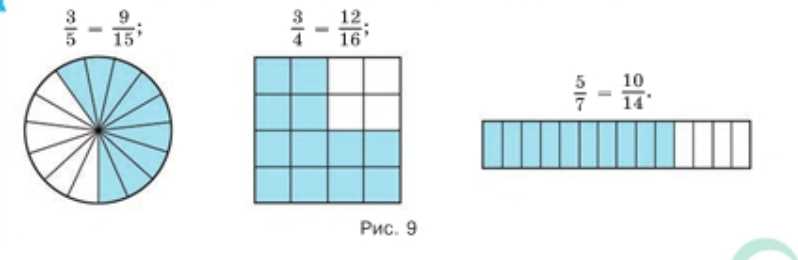
Используя рисунок 9, объясните, почему равны дроби:

Разделим круг на 5 равных частей и закрасим 3. Затем каждую из 5 частей делим ещё на 3 равные части. Всего получилось \(5\cdot 3=15\) частей, закрашено \(3\cdot 3=9\). Поэтому \(\frac{3}{5}=\frac{9}{15}\).

Разделим квадрат на 4 равные части и закрасим 3. Затем каждую четверть делим ещё на 4 равные части. Всего получилось \(4\cdot 4=16\) частей, закрашено \(3\cdot 4=12\). Поэтому \(\frac{3}{4}=\frac{12}{16}\).

Разделим прямоугольник на 7 равных частей и закрасим 5. Затем каждую часть делим ещё на 2 равные части. Всего получилось \(7\cdot 2=14\) частей, закрашено \(5\cdot 2=10\). Поэтому \(\frac{5}{7}=\frac{10}{14}\).

Представим круг, разделённый на 5 равных секторов, и из них закрашены 3. Это означает, что доля закраски равна \(\frac{3}{5}\). Теперь каждую из 5 частей мысленно делим ещё на 3 равные подчасти. Общее число одинаковых частей круга становится \(5\cdot 3=15\), а закрашенных подчастей становится \(3\cdot 3=9\). Так как мы только уточнили разбиение, не изменяя саму закрашенную долю, новая запись той же части круга — \(\frac{9}{15}\). Поскольку обе записи описывают одну и ту же величину, имеем равенство \(\frac{3}{5}=\frac{9}{15}\). Это иллюстрирует общий принцип: умножение числителя и знаменателя на одно и то же натуральное число не меняет значение дроби, так как и числитель, и знаменатель масштабируются одинаково.

Аналогично для квадрата: изначально квадрат делим на 4 равные четверти, закрашиваем 3. Это соответствует доле \(\frac{3}{4}\). Затем каждую четверть делим ещё на 4 равные части. Общее число мелких одинаковых частей квадрата становится \(4\cdot 4=16\), а закрашенных мелких частей — \(3\cdot 4=12\). Мы не добавили и не убавили закрашенную площадь, а лишь уточнили сетку разбиения, поэтому доля остаётся прежней, но может быть записана как \(\frac{12}{16}\). Следовательно, \(\frac{3}{4}=\frac{12}{16}\). Это конкретный пример свойства эквивалентности дробей при умножении числителя и знаменателя на одно и то же число: \(\frac{a}{b}=\frac{a\cdot k}{b\cdot k}\) для любого натурального \(k\), при \(b\neq 0\).

Для длинного прямоугольника мысленно делим его на 7 равных отрезков-частей и закрашиваем 5, что даёт \(\frac{5}{7}\). Затем каждую из 7 частей делим пополам, то есть на 2 равные части. Тогда всего станет \(7\cdot 2=14\) одинаковых мелких частей, а закрашенных мелких частей — \(5\cdot 2=10\). Доля закраски не меняется, потому что разбиение стало более детальным, но закрашенная часть осталась той же; новую запись этой же доли получаем как \(\frac{10}{14}\). Следовательно, \(\frac{5}{7}=\frac{10}{14}\). Эти три наглядных примера подтверждают единое правило: если одну и ту же геометрическую фигуру дробим на всё более мелкие равные части, одновременно пересчитывая и общее число частей, и число закрашенных, то отношение числителя к знаменателю сохраняется, а значит исходная дробь и полученная после одинакового умножения числителя и знаменателя описывают одну и ту же часть целого.