ГДЗ по Математике 6 Класс Часть 1 Номер 177 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

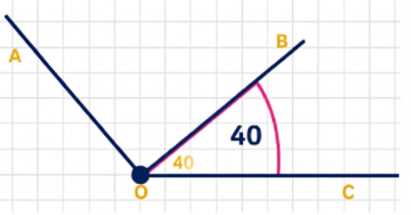
Постройте угол \(AOC\), равный \(130^\circ\). Проведите внутри угла \(AOC\) луч \(OB\) так, чтобы \(\angle BOC = 40^\circ\). Измерьте угол \(AOB\).

\( \angle AOC = 130^\circ, \quad \angle BOC = 40^\circ. \)

\( \angle AOB = \angle AOC — \angle BOC = 130^\circ — 40^\circ = 90^\circ. \)

Ответ: \( \angle AOB = 90^\circ. \)

Угол \( \angle AOC \) равен \( 130^\circ \), а угол \( \angle BOC \) равен \( 40^\circ \). Эти углы образованы лучами, исходящими из одной точки \( O \), и лежат на одной плоскости. При этом лучи \( OA \), \( OB \) и \( OC \) расположены так, что угол \( \angle AOC \) включает в себя угол \( \angle BOC \).

Чтобы найти угол \( \angle AOB \), необходимо понять, что он является частью угла \( \angle AOC \), из которого вычитается угол \( \angle BOC \). Это связано с тем, что угол \( \angle AOC \) состоит из двух частей: от \( OA \) до \( OB \) и от \( OB \) до \( OC \). Таким образом, угол \( \angle AOB \) можно найти, вычтя угол \( \angle BOC \) из угла \( \angle AOC \), то есть по формуле: \( \angle AOB = \angle AOC — \angle BOC \).

Подставляя числовые значения, получаем: \( \angle AOB = 130^\circ — 40^\circ = 90^\circ \). Это значит, что угол между лучами \( OA \) и \( OB \) равен \( 90^\circ \), то есть он является прямым углом. Следовательно, ответ: \( \angle AOB = 90^\circ \).