
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы: Жохов, Чесноков, Виленкин) — это практичный навигатор по ключевым темам стартового этапа курса, где закладывается основа математической компетентности: от освоения натуральных чисел и правил порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и простейшими уравнениями. Грамотно подготовленный решебник следует структуре учебника и помогает сформировать у школьника устойчивую привычку отслеживать логику рассуждений.
ГДЗ по Математике 6 Класс Часть 1 Номер 167 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
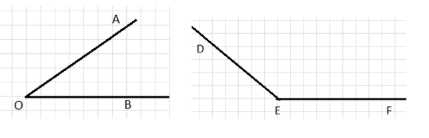
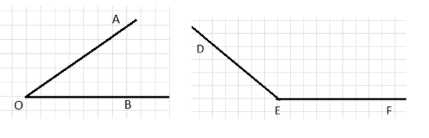
С помощью транспортира постройте \(\angle AOB = 35^\circ\) и \(\angle DEF = 140^\circ\).
Даны углы \(\angle AOB = 35^\circ\) и \(\angle DEF = 140^\circ\).
Угол \(\angle AOB\) острый, так как \(35^\circ < 90^\circ\). Угол \(\angle DEF\) тупой, так как \(140^\circ > 90^\circ\).
Ответ: \(\angle AOB\) — острый, \(\angle DEF\) — тупой.
Угол \( \angle AOB \) равен \( 35^\circ \). По определению, если угол меньше \( 90^\circ \), то он называется острым. В данном случае \( 35^\circ < 90^\circ \), следовательно, угол \( \angle AOB \) является острым углом. Острый угол характеризуется тем, что его величина находится в интервале от \( 0^\circ \) до \( 90^\circ \), то есть он меньше прямого угла. Угол \( \angle DEF \) равен \( 140^\circ \). Угол называется тупым, если его величина больше \( 90^\circ \), но меньше \( 180^\circ \). Поскольку \( 140^\circ > 90^\circ \) и \( 140^\circ < 180^\circ \), угол \( \angle DEF \) является тупым. Тупые углы больше прямого угла, но не достигают развернутого угла, который равен \( 180^\circ \). Таким образом, исходя из данных значений и определения видов углов, можно сделать вывод, что угол \( \angle AOB \) — острый, так как его величина меньше \( 90^\circ \), а угол \( \angle DEF \) — тупой, так как его величина больше \( 90^\circ \), но меньше \( 180^\circ \). Эти определения помогают классифицировать углы по их величинам и понять их геометрические свойства.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!