ГДЗ по Математике 6 Класс Часть 1 Номер 144 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

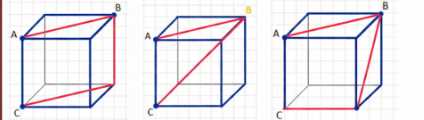
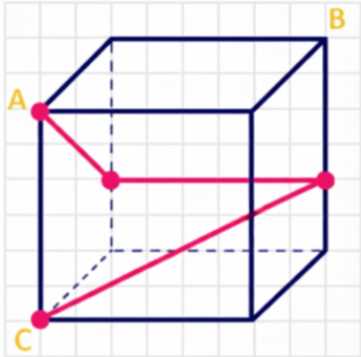
 На поверхности куба (рис. 6) найдите кратчайший путь:  

а) из точки \(A\) в точку \(C\) через точку \(B\);  

б) из точки \(A\) в точку \(C\), который пересекал бы все боковые рёбра куба, кроме ребра \(AC\).

а) Кратчайший путь из точки \( A \) в точку \( C \) через точку \( B \) — это сумма отрезков \( AB \) и \( BC \). В кубе длина ребра равна 1, тогда

\( AB = 1 \), \( BC = \sqrt{2} \).

Итого путь: \( AB + BC = 1 + \sqrt{2} \).

б) Кратчайший путь из точки \( A \) в точку \( C \), который пересекает все боковые ребра куба, кроме ребра \( AC \), — это диагональ грани куба, проходящая через точки \( A \) и \( C \) по поверхности. Длина этого пути равна диагонали квадрата со стороной 1:

\( AC = \sqrt{2} \).

а) Для нахождения кратчайшего пути из точки \( A \) в точку \( C \) через точку \( B \) необходимо рассмотреть два отрезка: отрезок \( AB \) и отрезок \( BC \). Поскольку \( A \), \( B \), и \( C \) — это вершины куба, длина ребра куба равна 1. Отрезок \( AB \) — это ребро куба, следовательно, его длина равна 1. Отрезок \( BC \) — это диагональ грани куба, которая соединяет две соседние вершины, не лежащие на одной стороне, поэтому длина \( BC \) равна длине диагонали квадрата со стороной 1. Она вычисляется по теореме Пифагора как \( \sqrt{1^2 + 1^2} = \sqrt{2} \).

Таким образом, общий путь из \( A \) в \( C \) через \( B \) равен сумме длин этих двух отрезков: \( AB + BC = 1 + \sqrt{2} \). Это и есть кратчайший путь, проходящий через точку \( B \), так как любые другие пути через \( B \) будут длиннее или равны этому.

б) Для нахождения кратчайшего пути из точки \( A \) в точку \( C \), который пересекает все боковые ребра куба, кроме ребра \( AC \), нужно представить, что путь должен проходить по поверхности куба, касаясь всех боковых рёбер, кроме ребра \( AC \). В этом случае кратчайший путь — это диагональ квадратной грани куба, соединяющая точки \( A \) и \( C \). Длина такой диагонали равна \( \sqrt{1^2 + 1^2} = \sqrt{2} \).

Этот путь короче, чем путь через точку \( B \), так как он не включает дополнительный отрезок, а проходит напрямую по поверхности куба, пересекает все боковые рёбра, кроме ребра \( AC \), и является минимальным по длине. Таким образом, искомая длина пути равна \( \sqrt{2} \).