ГДЗ по Математике 6 Класс Часть 1 Номер 107 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

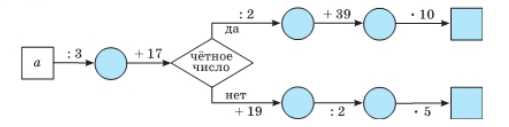
Найдите пропущенные числа, если \(a = 33; 42; 75\):

при \(a = 33\):
\(33 : 3 = 11;\)
\(11 + 17 = 28\) – четное;
\(28 : 2 = 14;\)
\(14 + 39 = 53;\)
\(53 \cdot 10 = 530.\)

при \(a = 42\):
\(42 : 3 = 14;\)
\(14 + 17 = 31\) – нечетное;
\(31 + 19 = 50;\)
\(50 : 2 = 25;\)
\(25 \cdot 5 = 125.\)

при \(a = 75\):
\(75 : 3 = 25;\)
\(25 + 17 = 42\) – четное;
\(42 : 2 = 21;\)
\(21 + 39 = 60;\)
\(60 \cdot 10 = 600.\)

Рассмотрим первый случай при \(a = 33\). Сначала делим число 33 на 3: \(33 : 3 = 11\). Это простая операция деления, где 33 разделено на 3, результат равен 11. Далее к полученному числу 11 прибавляем 17: \(11 + 17 = 28\). Число 28 — четное, так как делится на 2 без остатка. Проверяем это, деля 28 на 2: \(28 : 2 = 14\). Следующий шаг — прибавить к 14 число 39: \(14 + 39 = 53\). Число 53 — нечетное. Наконец, умножаем 53 на 10: \(53 \cdot 10 = 530\). Таким образом, для \(a = 33\) мы получили итоговое значение 530.

Рассмотрим второй случай при \(a = 42\). Сначала делим 42 на 3: \(42 : 3 = 14\). Это результат деления без остатка. К 14 прибавляем 17: \(14 + 17 = 31\). Число 31 — нечетное, так как оно не делится на 2 без остатка. Далее прибавляем к 31 число 19: \(31 + 19 = 50\). Число 50 — четное. Делим 50 на 2: \(50 : 2 = 25\). После этого умножаем 25 на 5: \(25 \cdot 5 = 125\). Таким образом, для \(a = 42\) итоговый результат равен 125.

Рассмотрим третий случай при \(a = 75\). Сначала делим 75 на 3: \(75 : 3 = 25\). Затем к 25 прибавляем 17: \(25 + 17 = 42\). Число 42 — четное, так как делится на 2 без остатка. Проверяем, деля 42 на 2: \(42 : 2 = 21\). Далее прибавляем к 21 число 39: \(21 + 39 = 60\). Число 60 — четное. В конце умножаем 60 на 10: \(60 \cdot 10 = 600\). Итоговый результат для \(a = 75\) равен 600.