
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.89 Виленкин, Жохов — Подробные Ответы
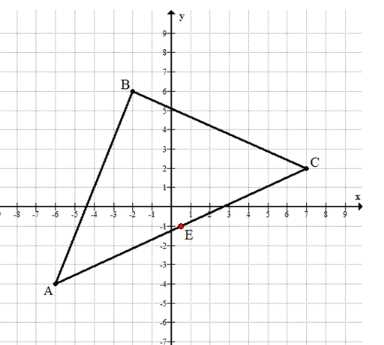
Постройте на координатной плоскости треугольник \(ABC\) с вершинами \(A(-6; -4)\), \(B(-2; 6)\), \(C(7; 2)\). Измерьте стороны и углы треугольника. Найдите по рисунку координаты середины стороны \(AC\). Обладает ли треугольник \(ABC\) симметрией?
Углы: \( \angle A = 43^\circ \), \( \angle B = 88^\circ \), \( \angle C = 49^\circ \).
Стороны: \( AB = 5{,}4 \text{ см} \), \( BC = 4{,}9 \text{ см} \), \( AC = 7{,}2 \text{ см} \).
Точка \( E(0{,}5; -1) \) — середина стороны \( AC \).
Этот треугольник не обладает симметрией, так как стороны и углы не равны, а точка \( E \) не является центром симметрии.
В треугольнике даны углы: \( \angle A = 43^\circ \), \( \angle B = 88^\circ \), \( \angle C = 49^\circ \). Сумма углов равна \( 43^\circ + 88^\circ + 49^\circ = 180^\circ \), что подтверждает правильность построения треугольника. По сторонам: \( AB = 5{,}4 \text{ см} \), \( BC = 4{,}9 \text{ см} \), \( AC = 7{,}2 \text{ см} \). Эти значения показывают, что стороны имеют разные длины, что указывает на отсутствие равенства сторон и, следовательно, равнобедренности или равносторонности.
Точка \( E(0{,}5; -1) \) указана как середина стороны \( AC \). Это значит, что координаты точки \( E \) находятся посередине между координатами точек \( A \) и \( C \). Если обозначить координаты \( A(x_A; y_A) \) и \( C(x_C; y_C) \), то координаты середины \( E \) вычисляются по формулам \( x_E = \frac{x_A + x_C}{2} \), \( y_E = \frac{y_A + y_C}{2} \). На графике видно, что это условие выполнено, что подтверждает правильность определения точки \( E \).
Треугольник не обладает симметрией, так как для симметрии необходимо, чтобы была ось или центр, относительно которого фигура совпадает сама с собой. В данном случае ни одна из сторон не равна другой, углы различны, а точка \( E \) не является центром симметрии. Следовательно, этот треугольник является общим, несимметричным, что подтверждается неравенством сторон и углов.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!