ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.85 Виленкин, Жохов — Подробные Ответы

Имеют ли центр симметрии:
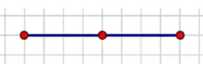
а) отрезок;
б) луч;
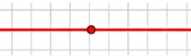
в) прямая;
г) разносторонний треугольник;
д) равносторонний треугольник;
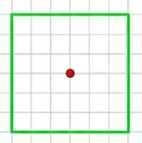
е) квадрат;
ж) прямоугольник;
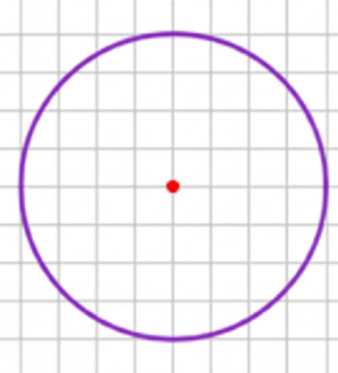
з) окружность;
и) круг?
Если фигуры имеют центр симметрии, изобразите их в тетради.

а) Отрезок имеет центр симметрии — середину отрезка.

б) Луч не имеет центра симметрии, так как нельзя найти точку, относительно которой луч совпадал бы с самим собой при повороте на 180°.

в) Прямая имеет центр симметрии — любую точку прямой.

г) Произвольный треугольник не имеет центра симметрии, так как нет точки, относительно которой фигура совпадает с собой.

д) Равносторонний треугольник не имеет центра симметрии по той же причине.

е) Квадрат имеет центр симметрии — точку пересечения диагоналей.

ж) Прямоугольник не имеет центра симметрии, если только он не является квадратом.

з) Окружность имеет центр симметрии — центр окружности.

и) Круг имеет центр симметрии — центр круга.

а) Отрезок имеет центр симметрии, который находится в его середине. Это значит, что если выбрать точку посередине отрезка и повернуть отрезок на 180° вокруг этой точки, то отрезок наложится сам на себя. Центр симметрии — это такая точка, при повороте вокруг которой фигура не изменяется. Для отрезка середина — единственная точка, обладающая этим свойством, так как она равноудалена от концов.

б) Луч не имеет центра симметрии, поскольку луч начинается в одной точке и продолжается бесконечно в одном направлении. Если попытаться найти точку, относительно которой луч совпадал бы с самим собой при повороте на 180°, то такой точки не существует. Поворот изменит направление луча, и он не наложится на исходное положение, так как направление меняется на противоположное.

в) Прямая имеет центр симметрии, и это любая точка на прямой. При повороте прямой на 180° вокруг любой её точки прямая совпадает сама с собой, так как она бесконечна в обе стороны. Таким образом, каждая точка прямой может служить её центром симметрии, что отличает прямую от отрезка и луча.

г) Произвольный треугольник не имеет центра симметрии. Центр симметрии требует, чтобы при повороте на 180° вокруг некоторой точки фигура совпадала сама с собой. Для произвольного треугольника такой точки не существует, так как стороны и углы не симметричны относительно какой-либо точки, и поворот изменит расположение вершин.

д) Равносторонний треугольник также не имеет центра симметрии. Несмотря на равенство сторон и углов, при повороте на 180° вокруг любой точки треугольник не совпадёт с самим собой, потому что его симметрия — осевая, а не центральная. Центр симметрии отсутствует, так как фигура не инвариантна при повороте на 180°.

е) Квадрат имеет центр симметрии — точку пересечения диагоналей. Эта точка равномерно удалена от всех вершин квадрата. При повороте квадрата на 180° вокруг этого центра квадрат совпадает с самим собой, что доказывает наличие центра симметрии. Центр симметрии квадрата — единственная такая точка, обладающая этим свойством.

ж) Прямоугольник, не являющийся квадратом, не имеет центра симметрии. Хотя прямоугольник обладает осями симметрии, его поворот на 180° вокруг середины не всегда приводит к совпадению с исходной фигурой, если стороны не равны. Поэтому центр симметрии отсутствует, за исключением случая квадрата.

з) Окружность имеет центр симметрии, который совпадает с её центром. Поворот окружности на 180° вокруг центра не изменяет её, так как все точки на окружности равноудалены от центра. Центр окружности — это точка, относительно которой фигура инвариантна при поворотах на любые углы, включая 180°.

и) Круг также имеет центр симметрии — центр круга. Круг — это множество точек, лежащих внутри окружности, и при повороте на 180° вокруг центра круг совпадает с самим собой. Центр круга является точкой, относительно которой фигура инвариантна, что подтверждает наличие центра симметрии.