ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.65 Виленкин, Жохов — Подробные Ответы

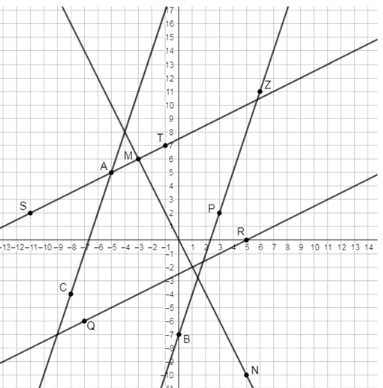
Отметьте точки \(M(-3; 6)\), \(N(5; -10)\), \(Q(-7; -6)\), \(R(5; 0)\), \(S(-11; 2)\), \(T(-1; 7)\), \(P(3; 2)\), \(Z(6; 11)\), \(A(-5; 5)\) и \(C(-8; -4)\) на координатной плоскости. Проведите прямые \(MN\), \(QR\), \(ST\), \(PZ\) и \(AC\). С помощью чертёжного треугольника и линейки найдите прямые, параллельные и перпендикулярные друг другу. Определите по рисунку координаты точки пересечения прямой \(PZ\) с осью \(y\) и прямой \(QR\) с осью \(x\). 

Отметим точки на координатной плоскости:
\(M(-3; 6)\), \(N(5; -10)\), \(Q(-7; -6)\), \(R(5; 0)\), \(S(-11; 2)\), \(T(-1; 7)\), \(P(3; 2)\), \(Z(6; 11)\), \(A(-5; 5)\), \(C(-8; -4)\).

Проведём прямые:
\(MN\), \(QR\), \(ST\), \(PZ\), \(AC\).

Определим параллельные прямые:
\(AC \parallel ZP\), \(ST \parallel QR\).

Определим перпендикулярные прямые:
\(ST \perp MN\), \(QR \perp MN\).

Координаты точек пересечения:
Прямая \(PZ\) пересекает ось \(y\) в точке \(B(0; -7)\).
Прямая \(QR\) пересекает ось \(x\) в точке \(R(5; 0)\).

На координатной плоскости отмечены точки \(M(-3; 6)\), \(N(5; -10)\), \(Q(-7; -6)\), \(R(5; 0)\), \(S(-11; 2)\), \(T(-1; 7)\), \(P(3; 2)\), \(Z(6; 11)\), \(A(-5; 5)\) и \(C(-8; -4)\). Эти точки служат опорными для построения прямых \(MN\), \(QR\), \(ST\), \(PZ\) и \(AC\). Каждая прямая соединяет соответствующие точки, образуя линии на плоскости, которые можно анализировать на параллельность и перпендикулярность.

Для проверки параллельности и перпендикулярности необходимо найти угловые коэффициенты (наклоны) прямых. Наклон прямой, проходящей через точки \((x_1; y_1)\) и \((x_2; y_2)\), вычисляется по формуле \(k = \frac{y_2 — y_1}{x_2 — x_1}\). Рассчитаем наклоны для прямых:

— Для \(AC\): \(k_{AC} = \frac{-4 — 5}{-8 — (-5)} = \frac{-9}{-3} = 3\).
— Для \(ZP\): \(k_{ZP} = \frac{11 — 2}{6 — 3} = \frac{9}{3} = 3\).

Так как \(k_{AC} = k_{ZP} = 3\), прямые \(AC\) и \(ZP\) параллельны.

— Для \(ST\): \(k_{ST} = \frac{7 — 2}{-1 — (-11)} = \frac{5}{10} = \frac{1}{2}\).
— Для \(QR\): \(k_{QR} = \frac{0 — (-6)}{5 — (-7)} = \frac{6}{12} = \frac{1}{2}\).

Значит, прямые \(ST\) и \(QR\) тоже параллельны.

— Для \(MN\): \(k_{MN} = \frac{-10 — 6}{5 — (-3)} = \frac{-16}{8} = -2\).

Проверим перпендикулярность с \(ST\) и \(QR\). Перпендикулярность двух прямых с наклонами \(k_1\) и \(k_2\) означает, что \(k_1 \cdot k_2 = -1\). Проверим:

— \(k_{ST} \cdot k_{MN} = \frac{1}{2} \cdot (-2) = -1\).
— \(k_{QR} \cdot k_{MN} = \frac{1}{2} \cdot (-2) = -1\).

Следовательно, \(ST \perp MN\) и \(QR \perp MN\).

Для нахождения точек пересечения прямых с осями координат используем уравнения прямых. Прямая \(PZ\) проходит через точки \(P(3; 2)\) и \(Z(6; 11)\), наклон \(k_{PZ} = \frac{11 — 2}{6 — 3} = 3\). Уравнение прямой в форме \(y = kx + b\) с подстановкой точки \(P\):

\(2 = 3 \cdot 3 + b = 2 — 9 = -7\).

Значит, уравнение \(PZ\) — \(y = 3x — 7\). Пересечение с осью \(y\) (при \(x = 0\)) будет в точке \(B(0; -7)\).

Прямая \(QR\) с точками \(Q(-7; -6)\) и \(R(5; 0)\) имеет наклон \(k_{QR} = \frac{0 — (-6)}{5 — (-7)} = \frac{6}{12} = \frac{1}{2}\). Уравнение прямой:

\(y = \frac{1}{2}x + b\).

Подставим точку \(R(5; 0)\):

\(0 = \frac{1}{2} \cdot 5 + b = -\frac{5}{2} = -2.5\).

Уравнение: \(y = \frac{1}{2}x — \frac{5}{2}\). Для пересечения с осью \(x\) при \(y = 0\):

\(0 = \frac{1}{2}x — \frac{5}{2} \frac{1}{2}x = \frac{5}{2} x = 5\).

Точка пересечения с осью \(x\) — \(R(5; 0)\).

Таким образом, параллельные прямые: \(AC \parallel ZP\), \(ST \parallel QR\). Перпендикулярные прямые: \(ST \perp MN\), \(QR \perp MN\). Точки пересечения с осями: \(PZ\) с осью \(y\) в \(B(0; -7)\), \(QR\) с осью \(x\) в \(R(5; 0)\).