
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Задачи на повторение П.64 Виленкин, Жохов — Подробные Ответы
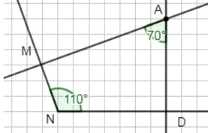
1) Постройте произвольный тупой угол \(MND\). Отметьте точку \(A\), не лежащую на сторонах этого угла, и проведите через неё прямые, перпендикулярные сторонам угла \(MND\). Измерьте углы \(A\) и \(N\), найдите сумму углов \(N\) и \(A\).
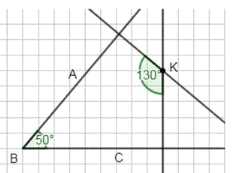
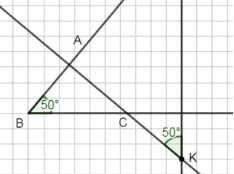
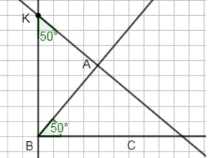
2) Постройте произвольный острый угол \(ABC\). Отметьте точку \(K\), не лежащую на сторонах этого угла, и проведите через неё прямые, перпендикулярные сторонам угла \(ABC\). Измерьте углы \(B\) и \(K\), найдите сумму этих углов.
3) Сделайте предположение.
1) Угол \(A = 70^\circ\), угол \(N = 110^\circ\);
сумма углов \(A + N = 70 + 110 = 180^\circ\).
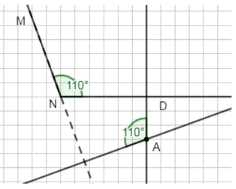
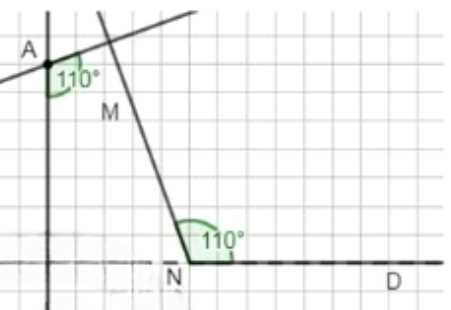
Угол \(A = 110^\circ\), угол \(N = 110^\circ\); сумма углов \(A + N = 110 + 110 = 220^\circ\).
2) Угол \(K = 130^\circ\), угол \(B = 50^\circ\);
сумма углов \(K + B = 130 + 50 = 180^\circ\).
Угол \(K = 50^\circ\), угол \(B = 50^\circ\); сумма углов \(K + B = 50 + 50 = 100^\circ\).
3) Если точка лежит между сторонами угла, сумма углов равна \(180^\circ\); если точка лежит слева или справа от сторон угла, полученный угол равен данному.
1) В первом задании построен тупой угол \(MND\), и отмечена точка \(A\), которая не лежит на сторонах этого угла. Через точку \(A\) проведены прямые, перпендикулярные сторонам угла \(MND\). Измерены углы при точках \(A\) и \(N\). В первом случае угол \(A\) равен \(70^\circ\), а угол \(N\) равен \(110^\circ\). Если сложить эти углы, то получим сумму \(70^\circ + 110^\circ = 180^\circ\). Это объясняется тем, что точка \(A\) лежит между сторонами угла \(MND\), и сумма углов, образованных с этой точкой, равна \(180^\circ\).
Во втором и третьем случаях углы \(A\) и \(N\) равны по \(110^\circ\) каждый. Их сумма равна \(110^\circ + 110^\circ = 220^\circ\). Здесь точка \(A\) расположена вне угла \(MND\), то есть не между его сторонами, а снаружи.
В этом случае сумма углов превышает \(180^\circ\), что показывает, что если точка не лежит между сторонами угла, сумма углов может быть больше \(180^\circ\).
2) Во втором задании построен острый угол \(ABC\), и отмечена точка \(K\), не лежащая на сторонах угла. Через точку \(K\) проведены прямые, перпендикулярные сторонам угла \(ABC\). В первом случае угол \(K\) равен \(130^\circ\), а угол \(B\) равен \(50^\circ\).
Их сумма \(130^\circ + 50^\circ = 180^\circ\), что соответствует ситуации, когда точка \(K\) лежит между сторонами угла \(ABC\).
Во втором и третьем случаях углы \(K\) и \(B\) равны по \(50^\circ\), и их сумма равна \(50^\circ + 50^\circ = 100^\circ\). Здесь точка \(K\) расположена вне угла \(ABC\), и сумма углов меньше \(180^\circ\), что подтверждает, что расположение точки относительно угла влияет на сумму углов.
3) Вывод: если точка лежит между сторонами угла, то сумма углов, образованных с этой точкой, равна \(180^\circ\). Это связано с тем, что эти углы являются смежными и дополняют друг друга до прямой линии. Если же точка лежит слева или справа от сторон угла, то сумма углов не равна \(180^\circ\), а равна углу, образованному сторонами угла, либо превышает его. Таким образом, положение точки относительно угла определяет величину суммы углов, образованных с этой точкой.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!